设A为严格对角占优矩阵 经过Gauss顺序消元法一步后 A约化为设C是矩阵A的逆矩阵A－1的近似解
设A为严格对角占优矩阵，经过Gauss顺序消元法一步后，A约化为设C是矩阵A的逆矩阵A－1的近似解，记R=＝
设C是矩阵A的逆矩阵A-1的近似解，记R=＝I－CA，如果‖R‖＜11，证明： (1)A和C均非奇异； (2)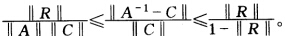
请帮忙给出正确答案和分析，谢谢！
参考解答
406***102
2024-11-17 10:53:23
正确答案：(1)因为‖R‖＜1因此I－R非奇异从而det(I－R)±0即det(C)det(A)±0所以A和C均非奇异。 (2)因为‖R‖＝‖I－CA‖＝‖A-1－C‖≤‖A-1－C‖‖A‖ 所以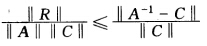
又因为‖A-1－C‖＝‖RA-1‖＝‖R(I－R)-1C‖ ≤‖R‖‖(I－R)-1‖‖C‖≤
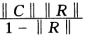所以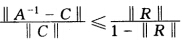
故命题成立。
(1)因为‖R‖＜1,因此I－R非奇异,从而det(I－R)±0,即det(C)det(A)±0,所以A和C均非奇异。(2)因为‖R‖＝‖I－CA‖＝‖A-1－C‖≤‖A-1－C‖‖A‖所以又因为‖A-1－C‖＝‖RA-1‖＝‖R(I－R)-1C‖≤‖R‖‖(I－R)-1‖‖C‖≤所以故命题成立。
相似问题
设χ∈Rn (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤‖χ‖∞； (3)‖
设χ∈Rn， (1)‖χ‖∞≤‖χ‖1≤n‖χ‖∞； (2)‖χ‖∞≤‖χ‖2≤‖χ‖∞； (3)‖χ‖2≤‖χ‖1≤‖χ‖2。请帮忙给出正确答案和分析，谢谢！
若要求分析结果的准确度为0．1％ 则用电光分析天平称取样品时至少应称取试样( )g。A．0.05B．
若要求分析结果的准确度为0．1％，则用电光分析天平称取样品时至少应称取试样( )g。A．0 05B．0 1C．0 2D．1 0请帮忙给出正确答案和分析，谢谢！
设f(χ)＝sinχ的函数表如下： 设f(χ)＝eχ χ∈[－1 1] 若用等距节点对eχ进行插值
设f(χ)＝sinχ的函数表如下： 设f(χ)＝eχ，χ∈[－1，1]，若用等距节点对eχ进行插值，要求截断误差不超过×1设f(χ)＝eχ，χ∈[－1，1]，若用等距
用0．10mol／L NaOH滴定0．10mol／L HAc至pH＝8．00 计算终点误差。[Ka(
用0．10mol／L NaOH滴定0．10mol／L HAc至pH＝8．00，计算终点误差。[Ka(HAc)＝1．8×10-5]请帮忙给出正确答案和分析，谢谢！
设初值问题设初始问题 试分别用Euler法和改进Euler法以步长h＝0．1进行求解 并与解析解y(
设初值问题设初始问题 试分别用Euler法和改进Euler法以步长h＝0．1进行求解，并与解析解y(χ)＝设初始问题 试分别用Euler法和改进Euler法以步长h＝0．1
