求一个正交变换将下列二次型化为标准形 并求出其正 负惯性指数及符号差。f=2x2+y2-4xy-4y

正确答案：二次型f的矩阵为则可得A的特征值为λ₁=4λ₂=1λ₃=-2。当λ₁=4时解齐次线性方程组(A-4E)x=0由可得特征向量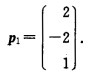当λ₂=1时解齐次线性方程组(A-E)x=0由可得特征向量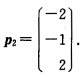当λ₃=-2时解齐次线性方程组(A+2E)x=0由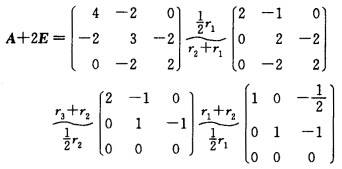可得特征向量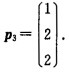对于实对称矩阵不同特征值对应的特征向量已正交故只需对其进行单位化有f=x^TAx=y^TAy=4x'²+y'²-2z'²且正负惯性指数分别为2和1符号差为1。
二次型f的矩阵为则可得A的特征值为λ1=4,λ2=1,λ3=-2。当λ1=4时,解齐次线性方程组(A-4E)x=0,由可得特征向量当λ2=1时,解齐次线性方程组(A-E)x=0,由可得特征向量当λ3=-2时,解齐次线性方程组(A+2E)x=0,由可得特征向量对于实对称矩阵,不同特征值对应的特征向量已正交,故只需对其进行单位化,有f=xTAx=yTAy=4x'2+y'2-2z'2,且正,负惯性指数分别为2和1,符号差为1。