设向量组α1＝(1 1 1 3)T α2＝(－1 一3 5 1)T α3＝(3 2 －1 p＋2)T
设向量组α1＝(1，1，1，3)T，α2＝(－1，一3，5，1)T，α3＝(3，2，－1，p＋2)T，α4＝(－2，－6，10，p)T， (1)户为何值时，该向量组线陛无关?并在此时将向量α＝(4，1，6，10)T用α1，α2，α3，α4线性表出； (2)p为何值时，该向量组线性相关?并在此时求出它的秩和一个极大线性无关组．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-15 14:40:28
正确答案：由于行列式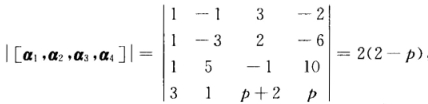
可见 (1)当p≠2时向量组α1α2α3α4线性无关．此时设 α＝x1α1x2α2x3α3x4α4对矩阵[α1α2α3α4｜α作初等行变换：
解得 x1＝2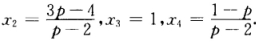
。 (2)当p＝2时向量组α1α2α3α4线性相关．此时向量组的秩等于3α1α2α3(或α1α3α4)为其一个极大线性无关组．
[分析由于向量的个数与维数相等，该向量组是否线性相关，可由其对应的行列式是否为零来判断．至于α用α1，α2，α3，α4线性表出，实质上是讨论方程组的解的问题．[评注一个向量是否可用一组向量线性表示，相当于对应的非齐次线性方程组是否有解，因此可以说，这两个问题是等价的．故在讨论与此相关的问题时，应注意它们之间的这种转换关系．
相似问题
设3阶矩阵已知向量组α1＝(1 2 －1 1) α2＝(2 0 t 0) α3＝(0 －4 5 －2
设3阶矩阵已知向量组α1＝(1，2，－1，1)，α2＝(2，0，t，0)，α3＝(0，－4，5，－2)的秩为2，则t＝________。已知向量组α1＝(1，2，－1，1)，α2＝(2
设矩阵Am×n的秩为r(A)=m＜n Em为m阶单位矩阵 下列结论中正确的是( )．A．A的任意m个
设矩阵Am×n的秩为r(A)=m＜n，Em为m阶单位矩阵，下列结论中正确的是( )．A．A的任意m个列向量必线性无关B．A的任意一个m阶子式不等于零C．若矩阵B满足BA
若方程组An×n=b有唯一解 A是该方程组的增广矩阵 则下列结论中成立的是( )．A．A的行向量组线
若方程组An×n=b有唯一解，A是该方程组的增广矩阵，则下列结论中成立的是( )．A．A的行向量组线性相关B．A的行向量组线性相关C．A的列向量组线性相关D．
设α1 α2 … αs是一组n维向量 则下列结论中 正确的是( )．A．若α1 α2 … αs不线性
设α1，α2，…，αs是一组n维向量，则下列结论中，正确的是( )．A．若α1，α2，…，αs不线性相关，就一定线性无关B．如果存在s个不全为零的数k1，k2
k为何值时 线性方程组已知下列非齐次线性方程组(I) (II)： (1)求解方程组(I) 用其导出组
k为何值时，线性方程组已知下列非齐次线性方程组(I)，(II)： (1)求解方程组(I)，用其导出组的基础已知下列非齐次线性方程组(I)，(II)： (1)求解方程
