已知已知正 负惯性指数均为1的二次型XTAX通过合同变换X=Py化为YT=BY 其中B为 则a=__
已知已知正、负惯性指数均为1的二次型XTAX通过合同变换X=Py化为YT=BY,其中B为,则a=_____.
已知正、负惯性指数均为1的二次型XTAX通过合同变换X=Py化为YT=BY,其中B为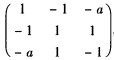 ,则a=_____.
,则a=_____.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:√
∵A的正、负惯性指数都为1,且A为三阶方阵.∴A必有一特征值为0.∴A=B∴RA=RB=2解得a=1
相似问题
设设N维向量α=(A 0 … 0 a)T a<0;E为n阶单位矩阵 矩阵 A=E—ααT 其中
设设N维向量α=(A,0,…,0,a)T,a<0;E为n阶单位矩阵,矩阵 A=E—ααT, , 其中A的逆矩阵为B,设N维向量α=(A,0,…,0,a)T,a<0;E为n阶
设已知AB—B=A 其中B= 则A=_______.已知AB—B=A 其中B= 则A=_______
设已知AB—B=A,其中B=,则A=_______.已知AB—B=A,其中B=,则A=_______.请帮忙给出正确答案和分析,谢谢!
设A为反对称矩阵 且|A|≠0 B可逆 A B为同阶方阵 A为A的伴随矩阵 则[ATA(BT)-1]
设A为反对称矩阵,且|A|≠0,B可逆,A、B为同阶方阵,A为A的伴随矩阵,则[ATA(BT)-1]=( ).A.B.C.D.请帮忙给出正确答案和分析,谢谢!
设向量组I:α1 α2 … αr 可由向量组Ⅱ:β1 β2 … βs线性表示 则下列命题正确的是A.
设向量组I:α1,α2,…,αr,可由向量组Ⅱ:β1,β2,…,βs线性表示,则下列命题正确的是A.若向量组I线性无关,则r≤s.B.若向量组I线性相关,则
设4阶方阵A=设矩阵A满足A2+A-4E=0 其中E为单位矩阵 则(A—E)-1=_______.设
设4阶方阵A=设矩阵A满足A2+A-4E=0,其中E为单位矩阵,则(A—E)-1=_______.设矩阵A满足A2+A-4E=0,其中E为单位矩阵,则(A—E)-1=_______.请












