设4阶方阵A＝设矩阵A满足A2＋A－4E＝0 其中E为单位矩阵 则(A—E)－1＝_______．设

参考解答

481***102

2024-11-15 22:09:23



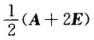
相似问题

• 已知A=(aij)n×n B=(bij)n×n…且有关系bij=系式正确的是( )．A．A(B+E)

  已知A=(aij)n×n，B=(bij)n×n…且有关系bij=系式正确的是( )．A．A(B+E)=BB．(B+E)A=BC．B(A—E)=AD．(E—A)B=A请帮忙给出正确答案和分析，谢谢！

• 设α1 α2 … αm均为以维列向量 那么 下列结论正确的是A．若k1α1＋k2α2＋…＋kmαm＝

  设α1，α2，…，αm均为以维列向量，那么，下列结论正确的是A．若k1α1＋k2α2＋…＋kmαm＝0，则α1，α2，…，αm线性相关．B．若对任意一组不全为零

• 设A为j阶方阵 A． A： A 表示A中三个列向量 则｜A｜=( )．A．｜A3 A2 A1｜B．｜

  设A为j阶方阵，A．，A：，A，表示A中三个列向量，则｜A｜=( )．A．｜A3,A2，A1｜B．｜A1+A2，A2+A3，A3+A1｜C．｜—A1，A2，A3｜D．｜A1，A1+A2，A1+A2+

• 设α1 α2 … αs均为n维向量 下列结论不正确的是A．若对于任意一组不全为零的数k1 k2 …

  设α1，α2，…，αs均为n维向量，下列结论不正确的是A．若对于任意一组不全为零的数k1，k2，…，ks，都有k1α1＋k2α2＋…＋ksαs≠0，则α1，α2，…，

• 设n阶方程A=(a1 a2 … an) B=(β1 β2 … βn) AB=(γ1 γ2 … γn)

  设n阶方程A=(a1，a2，…，an)，B=(β1，β2，…，βn)，AB=(γ1，γ2，…，γn)，记向量组(I)：α1，α2，…，αn，(Ⅱ)：β1，β2，…，βn，(Ⅲ)：γ1