证明若xs(t)(s=1 2 … m)分别是方程 设复值向量函数z(t)=x(t)＋iy(t)是线性
证明若xs(t)(s=1，2，…，m)分别是方程 设复值向量函数z(t)=x(t)＋iy(t)是线性微分方程组 的复值
设复值向量函数z(t)=x(t)+iy(t)是线性微分方程组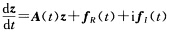 
的复值解，其中A(t)，fR(t)和，f1(t)都是实的．试证z(t)的实部x(t)和虚部y(t)分别是方程组 
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-14 06:13:44
正确答案：将z(t)=x(t)+iy(t)代入它所满足的方程组得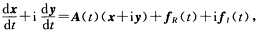
比较上式两边的实部和虚部即知所给结论成立．
将z(t)=x(t)+iy(t)代入它所满足的方程组得比较上式两边的实部和虚部即知所给结论成立．
相似问题
讨论非线性方程组 判断下列线性系统的平衡点的类型和稳定性 并画出相图：判断下列线性系统的平衡点的类型
讨论非线性方程组 判断下列线性系统的平衡点的类型和稳定性，并画出相图：判断下列线性系统的平衡点的类型和稳定性，并画出相图： 请帮忙给出正确答案
n阶行列式的反对角线上n个元素的乘积一定带负号吗?请帮忙给出正确答案和分析 谢谢！
n阶行列式的反对角线上n个元素的乘积一定带负号吗?请帮忙给出正确答案和分析，谢谢！
计算下列行列式：请帮忙给出正确答案和分析 谢谢！
计算下列行列式：请帮忙给出正确答案和分析，谢谢！
如何理解统计中的变量?请帮忙给出正确答案和分析 谢谢！
如何理解统计中的变量?请帮忙给出正确答案和分析，谢谢！
验证 设n×n矩阵函数A(t)在[α β]上连续 n维向量函数f(t x)在区域α≤t≤β ｜x｜＜
验证 设n×n矩阵函数A(t)在[α，β]上连续，n维向量函数f(t，x)在区域α≤t≤β，｜x｜＜∞上连续．证明初值问题设n×n矩阵函数A(t)在[α，β]上连续，n
