讨论非线性方程组 求出下述系统的平衡点 判断其类型和稳定性:求出下述系统的平衡点 判断其类型和稳定性
讨论非线性方程组 求出下述系统的平衡点,判断其类型和稳定性:
求出下述系统的平衡点,判断其类型和稳定性: 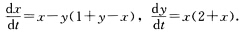
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:求解代数方程组 x-y(1+y-x)=0x(2+x)=0得到该系统有4个平衡点:O:(00)A1:(0-1)A2:(一2一2)A3:(-2-1). 对平衡点:O:(00)其线性部分的系数矩阵为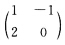 它有一对共轭复特征根
它有一对共轭复特征根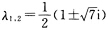 因此是不稳定焦点. 对平衡点:A1:(0一1)其线性部分的系数矩阵为
因此是不稳定焦点. 对平衡点:A1:(0一1)其线性部分的系数矩阵为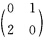 它有两个异号特征根
它有两个异号特征根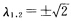 因此是鞍点不稳定.类似地通过分析平衡点处系统线性部分系数矩阵的特征值可知A2是稳定焦点;A3是鞍点不稳定.因而这几个平衡点都是双曲平衡点.
因此是鞍点不稳定.类似地通过分析平衡点处系统线性部分系数矩阵的特征值可知A2是稳定焦点;A3是鞍点不稳定.因而这几个平衡点都是双曲平衡点.
求解代数方程组x-y(1+y-x)=0,x(2+x)=0,得到该系统有4个平衡点:O:(0,0),A1:(0,-1),A2:(一2,一2),A3:(-2,-1).对平衡点:O:(0,0),其线性部分的系数矩阵为它有一对共轭复特征根,因此是不稳定焦点.对平衡点:A1:(0,一1),其线性部分的系数矩阵为它有两个异号特征根,因此是鞍点,不稳定.类似地,通过分析平衡点处系统线性部分系数矩阵的特征值可知A2是稳定焦点;A3是鞍点,不稳定.因而这几个平衡点都是双曲平衡点.
相似问题
证明Cauchy—Euler方程 1kg的重物悬挂在一弹簧上 使它伸长了后处于平衡位置.今自平衡位置
证明Cauchy—Euler方程 1kg的重物悬挂在一弹簧上,使它伸长了后处于平衡位置.今自平衡位置将重物1kg的重物悬挂在一弹簧上,使它伸长了后处于平衡位置.
计算下列n阶行列式:其中ai≠0 i=1 2 … n.其中ai≠0 i=1 2 … n.请帮忙给出正
计算下列n阶行列式:其中ai≠0,i=1,2,…,n.其中ai≠0,i=1,2,…,n.请帮忙给出正确答案和分析,谢谢!
求微分方程 在方程中如果没有假设g(y)≠0 讨论怎样用分离变量法来求解微分方程.在方程中如果没有假
求微分方程 在方程中如果没有假设g(y)≠0,讨论怎样用分离变量法来求解微分方程.在方程中如果没有假设g(y)≠0,讨论怎样用分离变量法来求解微分方程.
求齐次线性方程 求解方程组求解方程组 请帮忙给出正确答案和分析 谢谢!
求齐次线性方程 求解方程组求解方程组 请帮忙给出正确答案和分析,谢谢!
计算下述n阶行列式请帮忙给出正确答案和分析 谢谢!
计算下述n阶行列式请帮忙给出正确答案和分析,谢谢!












