设有3维列向量 试证明n维列向量组α1 α2 …αn线性无关的充分必要条件是试证明n维列向量组α1
设有3维列向量 试证明n维列向量组α1,α2,…αn线性无关的充分必要条件是
试证明n维列向量组α1,α2,…αn线性无关的充分必要条件是 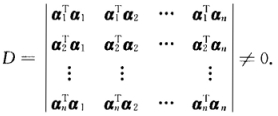
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:证明|A|≠0即可注意利用D=|ATA|=|A|2.
证明|A|≠0即可,注意利用D=|ATA|=|A|2.
相似问题
设向量组α1 α2 α3线性无关 则下列向量组中线性无关的是A.α1+α2 α2+α3 α3-α1.
设向量组α1,α2,α3线性无关,则下列向量组中线性无关的是A.α1+α2,α2+α3,α3-α1.B.α1+α2,α2+α3,α1+2α2+α3.C.α1+2α2,
设a1=(a1 a2 a3)T a2=(b1 b2 b3)T a3=(c1 c2 c3)T则三条直线
设a1=(a1,a2,a3)T,a2=(b1,b2,b3)T,a3=(c1,c2,c3)T则三条直线a1x+b1y+c1=0,a2x+b2y+c2=0,a3x+b3y+c3=0相交于一点的充分必要条件是( ).A.a1,a
设3阶矩阵已知R3中的两组基为 则由基α1 α2 α3到基β1 β2 β3的过渡矩阵为_______
设3阶矩阵已知R3中的两组基为 则由基α1,α2,α3到基β1,β2,β3的过渡矩阵为________.已知R3中的两组基为 则由基α1,α2,α3到基β1,β2,β3
设A是n阶矩阵 且A的行列式|A|=0 则A( ).A.必有一列元素全为0B.必有两列元素对应成比例
设A是n阶矩阵,且A的行列式|A|=0,则A( ).A.必有一列元素全为0B.必有两列元素对应成比例C.必有一列向量是其余列向量的线性组合D.任一列向量是其
从R2的基α1到基β1=862的过渡矩阵为_____.请帮忙给出正确答案和分析 谢谢!
从R2的基α1到基β1=862的过渡矩阵为_____.请帮忙给出正确答案和分析,谢谢!












