如图3—4所示 一个质量为m的物体从倾角为a的光滑斜面滑到质量为M的静止小车上.当物体落到小车上时
如图3—4所示,一个质量为m的物体从倾角为a的光滑斜面滑到质量为M的静止小车上.当物体落到小车上时,小车会获得多大的速度?设物体的最初位置距小车底板的高度为h,小车作无摩擦运动. 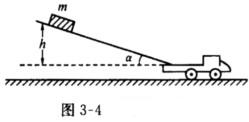
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:根据题意共有两个物理过程.第一个物理过程是物体自斜面落下直至落到小车底板上;第二过程是物体与小车的完全非弹性碰撞过程.两个过程之间的联系是物体落到斜面底部时的速度v0即物体与小车碰撞前的速度. 第一过程:取物体与地球为研究对象物体受重力及斜面支持力作用.外力(支持力)不做功故系统的机械能守恒有mgh=mv02/2.因此解得 第二过程:取物体与小车为系统.在完全非弹性碰撞过程中车与地面无摩擦水平方向的外力之和为零.因此水平方向的动量分量守恒.物体与小车碰撞前的速率是v0它沿水平方向速度大小为v0cosa.碰撞后物体与小车一起以速率v水平运动.在水平方向上应用动量守恒定律得 mv0cosa=(M+m)v (2)由式(2)解得
第二过程:取物体与小车为系统.在完全非弹性碰撞过程中车与地面无摩擦水平方向的外力之和为零.因此水平方向的动量分量守恒.物体与小车碰撞前的速率是v0它沿水平方向速度大小为v0cosa.碰撞后物体与小车一起以速率v水平运动.在水平方向上应用动量守恒定律得 mv0cosa=(M+m)v (2)由式(2)解得 将式(1)代入式(3)得
将式(1)代入式(3)得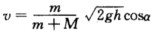
根据题意,共有两个物理过程.第一个物理过程是物体自斜面落下直至落到小车底板上;第二过程是物体与小车的完全非弹性碰撞过程.两个过程之间的联系是物体落到斜面底部时的速度v0,即物体与小车碰撞前的速度.第一过程:取物体与地球为研究对象,物体受重力及斜面支持力作用.外力(支持力)不做功,故系统的机械能守恒,有mgh=mv02/2.因此,解得第二过程:取物体与小车为系统.在完全非弹性碰撞过程中,车与地面无摩擦,水平方向的外力之和为零.因此,水平方向的动量分量守恒.物体与小车碰撞前的速率是v0,它沿水平方向速度大小为v0cosa.碰撞后物体与小车一起以速率v水平运动.在水平方向上应用动量守恒定律,得mv0cosa=(M+m)v(2)由式(2)解得将式(1)代入式(3),得
相似问题
在下面几种说法中 正确的说法是( ).A.波源不动时 波源的振动周期与波动的周期在数值上是不同的B.
在下面几种说法中,正确的说法是( ).A.波源不动时,波源的振动周期与波动的周期在数值上是不同的B.波源振动的速度与波速相同C.在波传播方向上的任一
两相干波源M N 振幅均为0.50 m 频率均为50Hz 初相差为π 波速为200 m.s-1。设M
两相干波源M、N,振幅均为0 50 m,频率均为50Hz,初相差为π,波速为200 m s-1。设M为坐标原点,且M的振动初相为0,N的坐标为30 m,如图7-6所示。 求
如图4-6所示 劲度系数为k的轻弹簧在质量为m的木块和外力(未画出)作用下 处于被压缩的状态 其压缩
如图4-6所示,劲度系数为k的轻弹簧在质量为m的木块和外力(未画出)作用下,处于被压缩的状态,其压缩量为x.当撤去外力后弹簧被释放,木块沿光滑斜面弹出
如图6-6所示 质量为m 半径为R的圆环静止于刀口上。令其在自身平面内做微小摆动。试证明圆环的运动为
如图6-6所示,质量为m,半径为R的圆环静止于刀口上。令其在自身平面内做微小摆动。试证明圆环的运动为简谐振动,并求振动周期。 请帮忙给出正确答案和分
一个质量为3kg的物体 初始位矢为 r=4i m 初始速度为v0=i+6j m·s-1.恒力f=5j
一个质量为3kg的物体,初始位矢为,r=4i m,初始速度为v0=i+6j m·s-1.恒力f=5j N作用在物体上.求3s后(1)物体动量的增量;(2)相对原点O的角动量的增












