两相干波源M N 振幅均为0.50 m 频率均为50Hz 初相差为π 波速为200 m.s-1。设M
两相干波源M、N,振幅均为0.50 m,频率均为50Hz,初相差为π,波速为200 m.s-1。设M为坐标原点,且M的振动初相为0,N的坐标为30 m,如图7-6所示。 求:(1)两波源的振动表达式;(2)在M、N之间,因两波叠加而静止的各点的位置。 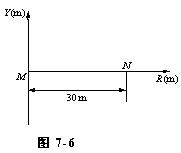
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)振动一般表达式为y=Acos(ωt+ψ0)=Acos(2πvt+ψ0) (1) 波源M的振幅为0.50 m频率为50Hz初相差为0。因此波源M的振动表达式为yM=0.50cos2π(50t)=0.50cos100πt (2) 波源N的振幅、频率均与M相同初相与M相差πψM=0则ψN=π。因此波源N的振动表达式为yN=0.50cos(100πt+π) (3)(2)在M、N之间任取一点坐标为r则两波传到该点的波程分别为rM=rrN=30-r两波传到该点的相位差为△ψ=(ψN-ψM)-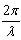 (rN-rM)=(ψN-ψM)-
(rN-rM)=(ψN-ψM)-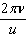 (rNrM)=
(rNrM)= =πr-14π(4)因干涉而静止不动的点满足干涉相消条件有△ψ=πr-14π=±(2k+1)πk=012 (5)解式(5)可得r=±(2k+1)+14k=012… (6)又由于0≤r≤30故在M、N之间因两波叠加而静止的各点的位置为r=135791113…29(m)
=πr-14π(4)因干涉而静止不动的点满足干涉相消条件有△ψ=πr-14π=±(2k+1)πk=012 (5)解式(5)可得r=±(2k+1)+14k=012… (6)又由于0≤r≤30故在M、N之间因两波叠加而静止的各点的位置为r=135791113…29(m)
(1)振动一般表达式为y=Acos(ωt+ψ0)=Acos(2πvt+ψ0)(1)波源M的振幅为0.50m,频率为50Hz,初相差为0。因此波源M的振动表达式为yM=0.50cos2π(50t)=0.50cos100πt(2)波源N的振幅、频率均与M相同,初相与M相差π,ψM=0,则ψN=π。因此波源N的振动表达式为yN=0.50cos(100πt+π)(3)(2)在M、N之间任取一点,坐标为r,则两波传到该点的波程分别为rM=r,rN=30-r,两波传到该点的相位差为△ψ=(ψN-ψM)-(rN-rM)=(ψN-ψM)-(rNrM)==πr-14π(4)因干涉而静止不动的点满足干涉相消条件,有△ψ=πr-14π=±(2k+1)π,k=0,1,2(5)解式(5)可得r=±(2k+1)+14,k=0,1,2…(6)又由于0≤r≤30,故在M、N之间,因两波叠加而静止的各点的位置为r=1,3,5,7,9,11,13,…,29(m)
相似问题
如图4-6所示 劲度系数为k的轻弹簧在质量为m的木块和外力(未画出)作用下 处于被压缩的状态 其压缩
如图4-6所示,劲度系数为k的轻弹簧在质量为m的木块和外力(未画出)作用下,处于被压缩的状态,其压缩量为x.当撤去外力后弹簧被释放,木块沿光滑斜面弹出
如图6-6所示 质量为m 半径为R的圆环静止于刀口上。令其在自身平面内做微小摆动。试证明圆环的运动为
如图6-6所示,质量为m,半径为R的圆环静止于刀口上。令其在自身平面内做微小摆动。试证明圆环的运动为简谐振动,并求振动周期。 请帮忙给出正确答案和分
一个质量为3kg的物体 初始位矢为 r=4i m 初始速度为v0=i+6j m·s-1.恒力f=5j
一个质量为3kg的物体,初始位矢为,r=4i m,初始速度为v0=i+6j m·s-1.恒力f=5j N作用在物体上.求3s后(1)物体动量的增量;(2)相对原点O的角动量的增
图7—4是干涉型消声器结构的原理图 利用这一结构可以消除噪声 当发动机排气噪声声波经管道到达点A时
图7—4是干涉型消声器结构的原理图,利用这一结构可以消除噪声,当发动机排气噪声声波经管道到达点A时,分成两路而在点B相遇,声波因干涉而相消.如果要
一列声波在空气中的波长是0.250m 波速是340m.s-1 当它进入另一种介质时 波长变为0.79
一列声波在空气中的波长是0 250m,波速是340m s-1,当它进入另一种介质时,波长变为0 790m,求声波在这种介质中的波速。请帮忙给出正确答案和分析,谢谢!












