已知设A为3阶实对称矩阵 A的秩r(A)＝2 且A 求 (1)A的特征值与特征向量； (2)矩阵A．
已知设A为3阶实对称矩阵，A的秩r(A)＝2，且A，求 (1)A的特征值与特征向量； (2)矩阵A．
设A为3阶实对称矩阵，A的秩r(A)＝2，且A
，求 (1)A的特征值与特征向量； (2)矩阵A．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-15 04:59:20
正确答案：(1)由r(A)＝2得A有特征值λ1＝0．又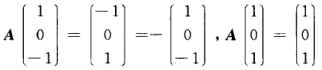
知A有特征值λ2＝－1λ3＝1且对应的特征向量分别为：α2＝(10－1)Tα3＝(101)T． 令λ1＝0对应的特征向量为α1＝(x1x2x3)T则α1与α2α3正交．于是 α1Tα2＝0α1Tα3＝0即
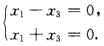解之得上述方程组的基础解系为(010)T故可取α1＝(010)T．所以λ1＝0λ2＝－1λ3＝1对应的特征向量分别为：k1α1k2α2k3α3．其中k1≠0k2≠0k3≠0．(2)记P＝(α1α2α3)＝
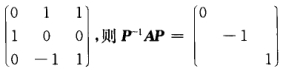得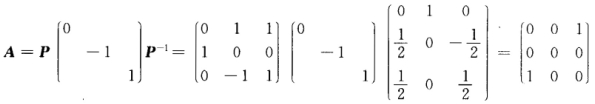
[分析利用特征值、特征向量的定义以及实对称矩阵不同特征值对应的特征向量正交进行求解．[评注若将α2，α3单位化，得．令Q＝(α2，η2，η3)，则Q为正交矩阵，且Q－1AQ＝QTAQ＝。
相似问题
设η1 η2 η3均为线性方程组AX=B的解向量 若ξ1=2η1-aη2+3bη3 ξ2=2aη1-
设η1，η2，η3均为线性方程组AX=B的解向量，若ξ1=2η1-aη2+3bη3，ξ2=2aη1-bη2+η3，ξ3=3bη1-3aη2+4η3也是AX=B的解，则a，b应满足( )．A．a=
已知二次型f(x1 x2 x3)=3x12+cx22+x32-2x1x2+2x1x3-2x2x3的秩
已知二次型f(x1，x2，x3)=3x12+cx22+x32-2x1x2+2x1x3-2x2x3的秩为2，则c的值为( )．A．0B．1C．2D．3请帮忙给出正确答案和分析，谢谢！
设向量α＝(a1 a2 … an)T β＝(b1 b2 … bn)T都是非零向量 且满足条件αTβ＝
设向量α＝(a1，a2，…，an)T，β＝(b1，b2，…，bn)T都是非零向量，且满足条件αTβ＝0，记n阶矩阵A＝αβT．求： (1)A2． (2)矩阵A的特征值．请帮忙
与向量α1=(1 1 一1 0) α2=(1 2 1 3) α3=(一1 1 6 6)都正交的向蛀为
与向量α1=(1，1，一1，0)，α2=(1，2，1，3)，α3=(一1，1，6，6)都正交的向蛀为_____．请帮忙给出正确答案和分析，谢谢！
计算下列积分其中C为正向圆周： (1)C：|z|=1； (2)C：|z－2|=1； (3)C：|z－
计算下列积分其中C为正向圆周： (1)C：|z|=1； (2)C：|z－2|=1； (3)C：|z－1|= (4)C：|z|=3．请帮忙给出正确答案和分析，谢谢！
