证明:对于任意初值χ0≠0 a≠0 迭代格式χn+1=χn(2-aχn) (n=0 1 2 …)收
证明:对于任意初值χ0≠0,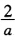 ,a≠0,迭代格式χn+1=χn(2-aχn) (n=0,1,2,…)收敛的充要条件是:|1-aχn|<1。
,a≠0,迭代格式χn+1=χn(2-aχn) (n=0,1,2,…)收敛的充要条件是:|1-aχn|<1。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为χn+1-χn=χn(1-aχn) =χn[1-aχn-1(2-aχn-1-1) =χn(1-aχn-1)2 ………… =χn(1-aχ0)2n 若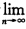 =χ*即
=χ*即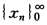 收敛则要求
收敛则要求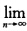 (1-aχ0)2n=0 即:|1-aχ0|<1。 反之若|1-aχ0|<1则对于任意的正整数P有 χn+p-χn=(χn+p-χn+p-1)+…+(χn+1-χn) =χn+p+1(1-aχ0)2n+p-1+…+χn(1-aχ0)2n 对于充分大的n上式右方趋于0即有 |χn+p-χn|<ε 由柯西(Cauchy)准则序列{χn0∞收敛。
(1-aχ0)2n=0 即:|1-aχ0|<1。 反之若|1-aχ0|<1则对于任意的正整数P有 χn+p-χn=(χn+p-χn+p-1)+…+(χn+1-χn) =χn+p+1(1-aχ0)2n+p-1+…+χn(1-aχ0)2n 对于充分大的n上式右方趋于0即有 |χn+p-χn|<ε 由柯西(Cauchy)准则序列{χn0∞收敛。
因为χn+1-χn=χn(1-aχn)=χn[1-aχn-1(2-aχn-1-1)=χn(1-aχn-1)2…………=χn(1-aχ0)2n若=χ*,即收敛,则要求(1-aχ0)2n=0即:|1-aχ0|<1。反之,若|1-aχ0|<1,则对于任意的正整数P,有χn+p-χn=(χn+p-χn+p-1)+…+(χn+1-χn)=χn+p+1(1-aχ0)2n+p-1+…+χn(1-aχ0)2n对于充分大的n,上式右方趋于0,即有|χn+p-χn|<ε由柯西(Cauchy)准则序列{χn0∞收敛。
相似问题
用Gauss顺序消元法解方程组并求系数矩阵的行列式的值。 请帮忙给出正确答案和分析 谢谢!
用Gauss顺序消元法解方程组并求系数矩阵的行列式的值。 请帮忙给出正确答案和分析,谢谢!
测定某样品含量 共测量了7次 其数据分别为79.54% 79.41% 79.43% 79.46% 7
测定某样品含量,共测量了7次,其数据分别为79.54%、79.41%、79.43%、79.46%、79.58%、79.34%、79.76%,计算平均值,平均偏差,相对平均偏
试用改进的Euler方法 计算定积分y(χ)=试用Adams的预估校正方法求解初始问题 (前几个初始
试用改进的Euler方法,计算定积分y(χ)=试用Adams的预估校正方法求解初始问题 (前几个初始值由试用Adams的预估校正方法求解初始问题 (前几个初始值
Hilbert矩阵讨论线性方程组 Jacobi迭代法及Gauss-Seidel迭代法的收敛性。讨论线
Hilbert矩阵讨论线性方程组 Jacobi迭代法及Gauss-Seidel迭代法的收敛性。讨论线性方程组 Jacobi迭代法及Gauss-Seidel迭代法的收敛性。请帮忙给出正确答案和分析,谢谢!
设定积分用Gauss-Legendre求积公式计算定积分 (1)I=∫-11 (n=3 4 5);
设定积分用Gauss-Legendre求积公式计算定积分 (1)I=∫-11,(n=3,4,5); (2)I=∫0πcosχdχ,(用Gauss-Legendre求积公式计算定积分 (1)I=∫-1












