实对称矩阵A是正定矩阵的充分必要条件为A的所有主子式都大于零．请帮忙给出正确答案和分析 谢谢！

正确答案：充分性 因为A的所有主子式全大于零那么顺序主子式必全大于零所以A是正定的必要性设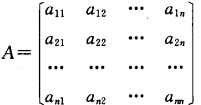而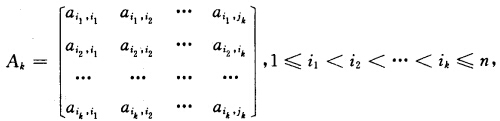为A的任一个是阶主子式｜A_k｜所对应的k阶实对称矩阵．因为A是正定的故二次型f(x₁x₂…x_n)=X^TAX对任意不全为零的实数x₁、x₂、…、x_n都有f(x₁、x₂…x_n)>0从而对不全为零的实数x_i1x_i2…x_in有f(0…x_i10…x_i2…x_ik…0)>0但对变量为x_i1x_i2…x_ik而矩阵为A_k的二次型g(x_i1…x_ik)有g(x_i1x_i2…x_ik)=f(0…x_i10…x_ik0…0)>0故g为正定二次型从而A_k是正定的所以｜A_k｜>0．
充分性因为A的所有主子式全大于零,那么顺序主子式必全大于零,所以A是正定的必要性设而为A的任一个是阶主子式｜Ak｜所对应的k阶实对称矩阵．因为A是正定的,故二次型f(x1,x2,…,xn)=XTAX,对任意不全为零的实数x1、x2、…、xn都有f(x1、x2…xn)>0,从而对不全为零的实数xi1,xi2…,xin有f(0,…,xi1,0,…,xi2,…,xik,…,0)>0但对变量为xi1,xi2…,xik而矩阵为Ak的二次型g(xi1,…,xik)有g(xi1,xi2,…,xik)=f(0,…,xi1,0,…,xik,0,…,0)>0,故g为正定二次型,从而Ak是正定的,所以｜Ak｜>0．