判定二次型：属于哪一种型?f(x1 x2 x3)=2x12+5x22+5x32+4x1x2－4x1x
判定二次型：
属于哪一种型?
f(x1，x2，x3)=2x12+5x22+5x32+4x1x2－4x1x3－8x2x3；
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-13 16:32:45
正确答案：二次型的矩阵是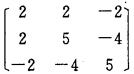
为实对称矩阵．
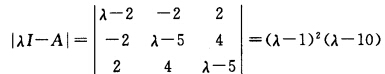由此可知征值λ=1、1、10对于λ=1解齐次方程组
得基础解系(2一10)与(201)正交化：β1=(210)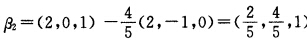
单位化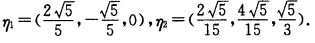
对于λ=10解齐次方程组
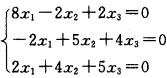得基础解系(12一2)．单位化得
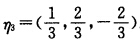令
则正交替换X=TY即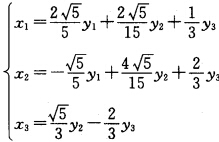
将原二次型化为：y12+y22+10y32．
二次型的矩阵是为实对称矩阵．由此可知征值λ=1、1、10对于λ=1解齐次方程组得基础解系(2,一1,0)与(2,0,1)正交化：β1=(2,1,0)单位化对于λ=10解齐次方程组得基础解系(1,2,一2)．单位化得令则正交替换X=TY,即将原二次型化为：y12+y22+10y32．
相似问题
设a·b＝3 a×b＝(1 1 1) 则a与b的夹角θ＝_______．请帮忙给出正确答案和分析 谢
设a·b＝3，a×b＝(1，1，1)，则a与b的夹角θ＝_______．请帮忙给出正确答案和分析，谢谢！
设事件Ai＝{第i次击中目标)(i＝1 2 3 4) B＝{击中次数大于2} 则事件A＝的含义是__
设事件Ai＝{第i次击中目标)(i＝1，2，3，4)，B＝{击中次数大于2}，则事件A＝的含义是________，的含义是________，的含义是________．请帮忙给出正确答案和分析，谢谢！
复数域上n元二次型(简称为复二次型)XAX能经过非退化线性替换化成下述形成的标准形：z12+z22+
复数域上n元二次型(简称为复二次型)XAX能经过非退化线性替换化成下述形成的标准形：z12+z22+…+zr2，其中r是二次型XAX的秩．这种形式的标准形称为XAX的规
某厂的回收溶液中含的浓度为6．6×10-4mol.L-1 在4．0L这种回收液中： (1)加入1．0
某厂的回收溶液中含的浓度为6．6×10-4mol L-1，在4．0L这种回收液中： (1)加入1．0L 0．010mol L-1的BaCl2溶液，能否生成沉淀? (2)生成沉淀后，残留
在一元线性回归数学模型y＝a＋bx＋ε ε～N(0 δ2)中( )．A．x是控制变量B．x是确定性变
在一元线性回归数学模型y＝a＋bx＋ε，ε～N(0，δ2)中( )．A．x是控制变量B．x是确定性变量C．ε是常数D．a，b，ε为待定常数此题为多项选择题。请帮忙
