利用Picard逐次逼近法求解初值问题 给定f(t)=(0 0 t)T 设三阶方阵A(t)在(一∞
利用Picard逐次逼近法求解初值问题 给定f(t)=(0，0，t)T ，设三阶方阵A(t)在(一∞，∞)上连续，已知方
给定f(t)=(0，0，t)T ，设三阶方阵A(t)在(一∞，∞)上连续，已知方程组 
对应的齐次方程组有基解矩阵 
试求所给方程组的通解及满足初始条件x(0)=0的解．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-14 05:47:24
正确答案：容易直接计算得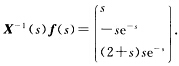
由常数变易公式原非齐次方程的通解为
其中c为任意常向量．即原方程组的通解为
其中C1C2C3为任意常数．由此而得满足初始条件x(0)=0的解为
容易直接计算得由常数变易公式,原非齐次方程的通解为其中c为任意常向量．即原方程组的通解为其中C1,C2,C3为任意常数．由此而得满足初始条件x(0)=0的解为
相似问题
试求初值问题 设是由不等式：T0＜t＜T1 ｜x｜＜∞所确定的区域．方程 的任一饱和解x=φ(t)均
试求初值问题 设是由不等式：T0＜t＜T1，｜x｜＜∞所确定的区域．方程 的任一饱和解x=φ(t)均有界，其中设是由不等式：T0＜t＜T1，｜x｜＜∞所确定的区
讨论非线性方程组 考虑下列两个方程组 其中A为常数值矩阵 B(t)为t≥0上的连续矩阵值函数 且满考
讨论非线性方程组 考虑下列两个方程组 其中A为常数值矩阵，B(t)为t≥0上的连续矩阵值函数，且满考虑下列两个方程组 其中A为常数值矩阵，B(t)为t≥0
(89年考研题)若齐次线性方程组只有零解则λ应满足__________.请帮忙给出正确答案和分析 谢
(89年考研题)若齐次线性方程组只有零解则λ应满足__________ 请帮忙给出正确答案和分析，谢谢！
试求初值问题 证明：若把Euler折线作如下的修正：证明：若把Euler折线作如下的修正： 请帮忙给
试求初值问题 证明：若把Euler折线作如下的修正：证明：若把Euler折线作如下的修正： 请帮忙给出正确答案和分析，谢谢！
设函数f(x)连续 g(x)满足局部Lipschitz条件 证明方程组 给定区间[a b]上的三个连
设函数f(x)连续，g(x)满足局部Lipschitz条件，证明方程组 给定区间[a，b]上的三个连续函数u(t)，∮(t给定区间[a，b]上的三个连续函数u(t)，∮(t)和λ(t)
