试求初值问题 讨论下列初值问题的解的最大存在区间(α β)及当t→α＋和t→β一时解的性质：讨论下列
试求初值问题 讨论下列初值问题的解的最大存在区间(α，β)及当t→α＋和t→β一时解的性质：
讨论下列初值问题的解的最大存在区间(α，β)及当t→α+和t→β一时解的性质：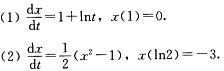 
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-14 04:52:14
正确答案：(1)容易由变量分离法求得该初值问题的解为x(t)=tInt．因此该初值问题的解的最大存在区间为(0+∞)且当t→0+时解趋于0当t→+∞时解趋于+∞． (2)容易由变量分离法求得该初值问题的解为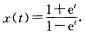
因此该初值问题的解的最大存在区间为(0+∞)且当t→0+时解趋于一∞当t→+∞时解趋于一1．
(1)容易由变量分离法求得该初值问题的解为x(t)=tInt．因此该初值问题的解的最大存在区间为(0,+∞)且当t→0+时解趋于0,当t→+∞时解趋于+∞．(2)容易由变量分离法求得该初值问题的解为因此该初值问题的解的最大存在区间为(0,+∞)且当t→0+时解趋于一∞,当t→+∞时解趋于一1．
相似问题
大量观察法请帮忙给出正确答案和分析 谢谢！
大量观察法请帮忙给出正确答案和分析，谢谢！
渗铝剂Alcl3和还原剂SnCl2的晶体均易潮解 主要是因为均易与水反应。试分别用化学方程式表示之。
渗铝剂Alcl3和还原剂SnCl2的晶体均易潮解，主要是因为均易与水反应。试分别用化学方程式表示之。要把SnCl2的晶体配制成溶液，如何配制才能得到澄清的溶液
计算下述n阶行列式请帮忙给出正确答案和分析 谢谢！
计算下述n阶行列式请帮忙给出正确答案和分析，谢谢！
讨论非线性方程组 设α β γ δ ε都是正数 x≥0 y≥0 求出方程组 的所有定常解并讨论其稳定
讨论非线性方程组 设α，β，γ，δ，ε都是正数，x≥0，y≥0，求出方程组 的所有定常解并讨论其稳定性．设α，β，γ，δ，ε都是正数，x≥0，y≥0，
证明若xs(t)(s=1 2 … m)分别是方程 求Airy方程 在t=0处展开的幂级数解．求Air
证明若xs(t)(s=1，2，…，m)分别是方程 求Airy方程 在t=0处展开的幂级数解．求Airy方程 在t=0处展开的幂级数解．请帮忙给出正确答案和分析，谢谢！
