设A为4阶实对称矩阵 且A2＋A＝0 若A的秩为3 则A与A相似于A．B．C．D．请帮忙给出正确答案
设A为4阶实对称矩阵，且A2＋A＝0，若A的秩为3，则A与A相似于
A．
B．
C．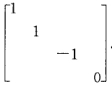
D．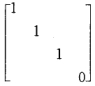
请帮忙给出正确答案和分析，谢谢！
参考解答
406***102
2024-11-15 03:23:57
正确答案：D
[详解设λ为A的特征值，由A2＋A＝0，知特征方程为λ2＋λ＝0，所以λ＝－1或0．由于A为实对称矩阵，故A可相似对角化，即A～A，r(A)＝r(A)＝3，因此，应选(D)．[评注1若A可对角化，则r(A)＝矩阵A的非零特征值的个数．[评注2本题由A2＋A＝0即可得到A可对角化，因此题设条件A为实对称矩阵可去掉．
相似问题
求矩阵已知向量α＝(1 k 1)T是矩阵的逆矩阵A－1的特征向量 试求常数k的值．已知向量α＝(1
求矩阵已知向量α＝(1，k，1)T是矩阵的逆矩阵A－1的特征向量，试求常数k的值．已知向量α＝(1，k，1)T是矩阵的逆矩阵A－1的特征向量，试求常数k的值．请
二次型f(x1 x2 … xn)=XTAX 其中AT=A 则f(x1 x2 … xn)为正定二次型的
二次型f(x1，x2，…，xn)=XTAX，其中AT=A，则f(x1，x2，…，xn)为正定二次型的充分必要条件是( )．A．存在n阶矩阵C，使A=CTCB．存在正交矩阵Q，使QTAQ=d
设A为m×s矩阵 B为s×n矩阵 要使ABx=0与Bx=0为同解方程组的充分条件是( )．A．RA=
设A为m×s矩阵，B为s×n矩阵，要使ABx=0与Bx=0为同解方程组的充分条件是( )．A．RA=mB．RA=sC．rB=sD．rB=n请帮忙给出正确答案和分析，谢谢！
设3阶矩阵A满足Aαi＝iαi(i＝1 2 3) 其中列向量α1＝(1 2 2)T α2＝(2 －2
设3阶矩阵A满足Aαi＝iαi(i＝1，2，3)，其中列向量α1＝(1，2，2)T，α2＝(2，－2，1)T，α3＝(－2，－1，2)T，试求矩阵A．请帮忙给出正确答案和分析，谢谢！
设3阶实对称矩阵A的特征值是1 2 3；矩阵A的属于特征值1 2的特征向量分别是α1＝(－1 －1
设3阶实对称矩阵A的特征值是1，2，3；矩阵A的属于特征值1，2的特征向量分别是α1＝(－1，－1，1)T，α2＝(1，－2，－1)T． (1)求A的属于特征值3的特征向
