设3阶矩阵A满足Aαi＝iαi(i＝1 2 3) 其中列向量α1＝(1 2 2)T α2＝(2 －2
设3阶矩阵A满足Aαi＝iαi(i＝1，2，3)，其中列向量α1＝(1，2，2)T，α2＝(2，－2，1)T，α3＝(－2，－1，2)T，试求矩阵A．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***102
2024-11-15 03:18:36
正确答案：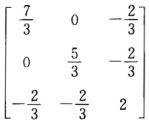
相似问题
设3阶实对称矩阵A的特征值是1 2 3；矩阵A的属于特征值1 2的特征向量分别是α1＝(－1 －1
设3阶实对称矩阵A的特征值是1，2，3；矩阵A的属于特征值1，2的特征向量分别是α1＝(－1，－1，1)T，α2＝(1，－2，－1)T． (1)求A的属于特征值3的特征向
设n阶实对称矩阵A的属于特征值λ的特征向量为α P为n阶可逆矩阵 则矩阵(P-1AP)T的属于特征值
设n阶实对称矩阵A的属于特征值λ的特征向量为α，P为n阶可逆矩阵，则矩阵(P-1AP)T的属于特征值λ的特征向量为________．请帮忙给出正确答案和分析，谢谢！
染色单体(chromatid)请帮忙给出正确答案和分析 谢谢！
染色单体(chromatid)请帮忙给出正确答案和分析，谢谢！
简述真核细胞和原核细胞的主要区别。请帮忙给出正确答案和分析 谢谢！
简述真核细胞和原核细胞的主要区别。请帮忙给出正确答案和分析，谢谢！
求矩阵设A为n阶矩阵 λ1和λ2是A的两个不同的特征值 X1 X2是分别属于λ1和λ2的特征向量 试
求矩阵设A为n阶矩阵，λ1和λ2是A的两个不同的特征值，X1，X2是分别属于λ1和λ2的特征向量，试证明X1＋X2设A为n阶矩阵，λ1和λ2是A的两个不同的特征值
