已知离散系统的系统函数如下。 试用MATLAB实现下列分析过程: (1)求出系统的零极点位置。 (
已知离散系统的系统函数如下。 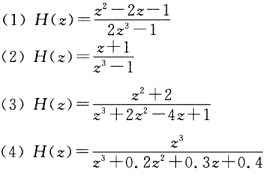 试用MATLAB实现下列分析过程: (1)求出系统的零极点位置。 (2)绘出系统的零极点图,根据零极点图判断系统的稳定性。 (3)绘出系统单位响应的时域波形,并分析系统稳定性与系统单位响应时域特性的关系。
试用MATLAB实现下列分析过程: (1)求出系统的零极点位置。 (2)绘出系统的零极点图,根据零极点图判断系统的稳定性。 (3)绘出系统单位响应的时域波形,并分析系统稳定性与系统单位响应时域特性的关系。
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:程序清单如下。 A1=[200一1; B1=[01一2一1; A2=[100一1; B2=[0011; A3=[12一41; B3=[0102; A4=[10.20.30.4; B4=[1000; [h1nn=impz(BlA150); [h2nn=impz(B2A250); [h3nn=impz(B3A350); [h4nn=impz(B4A450); figure(1) subplot(221); zplane(B1A1); subplot(222);stem(nhln′.′); axis([050一11) subplot(223); zplane(B2A2); subplot(224);stem(nh2n′.′); axis([050一12) figure(2) subplot(221); zplane(B3A3); subplot(222); stem(nh3n′.′); axis([050一10000001000000) subplot(223); zplane(B4A4); subplot(224); stem(nh4n′.′); axis([050一11) 程序运行结果如图2.10所示。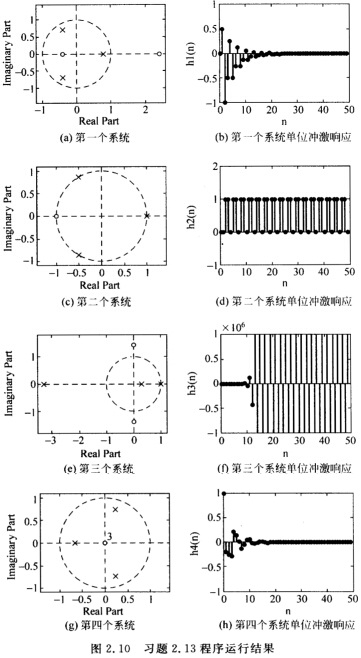 第一个系统的极点全部都在单位网内系统是稳定的因此单位冲激响应是收敛的。第二个系统的极点全部都在单位圆上系统处于临界状态因此单位冲激响应是阶跃函数的形式。第三个系统的极点都在单位圆外的系统是不稳定的因此单位冲激响应是发散的。第四个系统的极点全部都在单位圆内系统是稳定的因此单位冲激响应是收敛的。
第一个系统的极点全部都在单位网内系统是稳定的因此单位冲激响应是收敛的。第二个系统的极点全部都在单位圆上系统处于临界状态因此单位冲激响应是阶跃函数的形式。第三个系统的极点都在单位圆外的系统是不稳定的因此单位冲激响应是发散的。第四个系统的极点全部都在单位圆内系统是稳定的因此单位冲激响应是收敛的。
程序清单如下。A1=[2,0,0,一1;B1=[0,1,一2,一1;A2=[1,0,0,一1;B2=[0,0,1,1;A3=[1,2,一4,1;B3=[0,1,0,2;A4=[1,0.2,0.3,0.4;B4=[1,0,0,0;[h1n,n=impz(Bl,A1,50);[h2n,n=impz(B2,A2,50);[h3n,n=impz(B3,A3,50);[h4n,n=impz(B4,A4,50);figure(1)subplot(2,2,1);zplane(B1,A1);subplot(2,2,2);stem(n,hln,′.′);axis([0,50,一1,1)subplot(2,2,3);zplane(B2,A2);subplot(2,2,4);stem(n,h2n,′.′);axis([0,50,一1,2)figure(2)subplot(2,2,1);zplane(B3,A3);subplot(2,2,2);stem(n,h3n,′.′);axis([0,50,一1000000,1000000)subplot(2,2,3);zplane(B4,A4);subplot(2,2,4);stem(n,h4n,′.′);axis([0,50,一1,1)程序运行结果如图2.10所示。第一个系统的极点全部都在单位网内,系统是稳定的,因此单位冲激响应是收敛的。第二个系统的极点全部都在单位圆上,系统处于临界状态,因此单位冲激响应是阶跃函数的形式。第三个系统的极点都在单位圆外的,系统是不稳定的,因此单位冲激响应是发散的。第四个系统的极点全部都在单位圆内,系统是稳定的,因此单位冲激响应是收敛的。
相似问题
某他励电动机 PN=30 kW UaN=440 V IaN/sub>=82.5 A nN=1 000
某他励电动机,PN=30 kW,UaN=440 V,IaN sub>=82.5 A,nN=1 000 r/min。拖动恒功率负载运行,采用改变电枢电阻调速。求转速降低至n=800 r/min
一台并励直流电动机 额定功率PN=2.2 kW 额定电压UN=220 V 额定效率ηN=80% 额定
一台并励直流电动机,额定功率PN=2.2 kW,额定电压UN=220 V,额定效率ηN=80%,额定转速nN=750 r/min,电枢电路电阻Ra=0.2 Ω,励磁电路电阻Rf=2
保持If不变 是否就不变?请帮忙给出正确答案和分析 谢谢!
保持If不变,是否就不变?请帮忙给出正确答案和分析,谢谢!
某S3工作制的电动机 满载损耗比α=0.8 负载持续率为25% 它的额定功率为42 kW。求负载持续
某S3工作制的电动机,满载损耗比α=0.8,负载持续率为25%,它的额定功率为42 kW。求负载持续率分别为15%、40%和60%时,该电机允许输出的功率。请帮
原始信号x(n)=sin(πn/8)中加入随机噪声信号 再用差分方程 y(n)一0.8y(n一1)=
原始信号x(n)=sin(πn/8)中加入随机噪声信号,再用差分方程 y(n)一0.8y(n一1)=x(n)+0.2x(n一1) 应用filter函数对合成的信号进行滤波,并对滤波前后












