证明设S是Rn中非空凸集 f是定义在S上的实函数．若对任意的x(1) x(2)∈S及每一个数λ∈(0
证明设S是Rn中非空凸集，f是定义在S上的实函数．若对任意的x(1)，x(2)∈S及每一个数λ∈(0，1)，均有
设S是Rn中非空凸集，f是定义在S上的实函数．若对任意的x(1)，x(2)∈S及每一个数λ∈(0，1)，均有 f(λx(1)+(1一λ)x(2))≤max{f(x(1))，f(x(2))}，则称f为拟凸函数． 试证明：若f(x)是凸集S上的拟凸函数，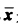
是f(x)在S上的严格局部极小点，则
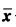也是f(x)在S上的严格全局极小点．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-14 18:38:45
正确答案：用反证法．设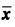
是严格局部极小点即存在
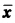的δ邻域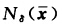
对于每个x∈S ∩
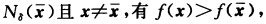但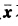
不是严格全局极小点即存在点
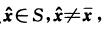使得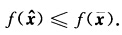
由于f(x)是凸集S上的拟凸函数对每个λ∈(01)有
用反证法．设是严格局部极小点,即存在的δ邻域,对于每个x∈S∩,但不是严格全局极小点,即存在点,使得由于f(x)是凸集S上的拟凸函数,对每个λ∈(0,1)有
相似问题
计算积分已知调和函数u(x y)=y3－3x2y 再求v(x y) 使f(z)=u(x y)＋iv(
计算积分已知调和函数u(x，y)=y3－3x2y，再求v(x，y)，使f(z)=u(x，y)＋iv(x，y)解析．已知调和函数u(x，y)=y3－3x2y，再求v(x，y)，使f(z)=u(x，y)+iv(x
问分式线性映射如果分式线性映射将z平面上的直线映射成w平面上的单位圆周 那么它的系数应满足什如果分式
问分式线性映射如果分式线性映射将z平面上的直线映射成w平面上的单位圆周，那么它的系数应满足什如果分式线性映射将z平面上的直线映射成w平面上的单位圆
计算下列积分求由下列条件确定的解析函数f(z)=u(x y)＋iv(x y) (1)u(x y)=x
计算下列积分求由下列条件确定的解析函数f(z)=u(x，y)＋iv(x，y) (1)u(x，y)=x2＋xy－y2，f(i)=－1＋求由下列条件确定的解析函数f(z)=u(x，y)+iv(x，y)
证明Ax≤0 cTx＞0有解．其中 请帮忙给出正确答案和分析 谢谢！
证明Ax≤0，cTx＞0有解．其中 请帮忙给出正确答案和分析，谢谢！
求图8．1所示周期函数的拉氏变换． 求下列函数的拉氏变换． (1)f(t)=t3－2t＋2； (2)
求图8．1所示周期函数的拉氏变换． 求下列函数的拉氏变换． (1)f(t)=t3－2t＋2； (2)f(求下列函数的拉氏变换． (1)f(t)=t3－2t+2； (2)f(t)=1－tet
