设有微分方程y-2y=ψ(x) 其中试求在(-∞ +∞)内的连续函数y=y(x) 使之在(-∞ 1)
设有微分方程y-2y=ψ(x),其中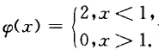 试求在(-∞,+∞)内的连续函数y=y(x),使之在(-∞,1)和(1,+∞)内都满足所给方程,满足条件y(0)=0.
试求在(-∞,+∞)内的连续函数y=y(x),使之在(-∞,1)和(1,+∞)内都满足所给方程,满足条件y(0)=0.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: ;
;
;
相似问题
某可控硅控制线路中 流过负载R的电流i(t)为其中ω=2π/T t。称为触发时间 如果T=0.02s
某可控硅控制线路中,流过负载R的电流i(t)为其中ω=2π/T,t。称为触发时间,如果T=0.02s, (1)当触发时间t。=0.0025s时,求[0,T/2]内电流的平
设函数f(x) g(x)满足f(x)=g(x) g(x)=2e2x-f(x) 且f(0)=0 g(0
设函数f(x),g(x)满足f(x)=g(x),g(x)=2e2x-f(x),且f(0)=0,g(0)=2,求。请帮忙给出正确答案和分析,谢谢!
求微分方程的通解.请帮忙给出正确答案和分析 谢谢!
求微分方程的通解.请帮忙给出正确答案和分析,谢谢!
设f(x)在(-∞ +∞)上连续 且 证明:(1)若f(x)为偶函数 则F(x)也是偶函数; (2)
设f(x)在(-∞,+∞)上连续,且 证明:(1)若f(x)为偶函数,则F(x)也是偶函数; (2)若f(x)是单调减少函数,则F(x)也是单调减少函数.请帮忙给出正确答案和分析,谢谢!
在上半平面求一条向上凹的曲线 其上任一点P(x y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(
在上半平面求一条向上凹的曲线,其上任一点P(x,y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点),且曲线在点(1,1)处的切线与x轴












