已知矩阵已知矩阵 则秩r(A)＝______．已知矩阵 则秩r(A)＝______．请帮忙给出正确答
已知矩阵已知矩阵 则秩r(A)＝______．
已知矩阵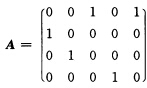
则秩r(A)＝______．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-13 08:41:23
正确答案：4
容易看出，所给矩阵A中4行都是非零行，第1行首非零元素1在第3列，第2行首非零元素1在第1列，第3行首非零元素1在第2列，第4行首非零元素1在第4列，它们在不同列，因而矩阵A为阶梯形矩阵，又由于其非零行为4行，说明秩r(A)＝4，于是应将“4”直接填在空内．
相似问题
已知矩阵已知三阶方阵 (1)判别三阶方阵A是否可逆? (2)若三阶方阵A可逆 则求逆矩阵A－1．已知
已知矩阵已知三阶方阵 (1)判别三阶方阵A是否可逆? (2)若三阶方阵A可逆，则求逆矩阵A－1．已知三阶方阵 (1)判别三阶方阵A是否可逆? (2)若三阶方阵A
已知线性方程组 已知线性方程组 (1)求增广矩阵的秩r()与系数矩阵A的秩r(A)； (2)判别此线
已知线性方程组 已知线性方程组 (1)求增广矩阵的秩r()与系数矩阵A的秩r(A)； (2)判别此线性已知线性方程组 (1)求增广矩阵的秩r()与系数矩阵A的秩r(
已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系； (2)若此齐次线性方程组存在基础
已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系； (2)若此齐次线性方程组存在基础解系，则求它的一个基础解系．请帮忙给出正确答案和
已知三阶行列式D＝已知三阶行列式D中第1行的元素自左向右依次为－1 1 2 它们的代数余子式分别为3
已知三阶行列式D＝已知三阶行列式D中第1行的元素自左向右依次为－1，1，2，它们的代数余子式分别为3，4已知三阶行列式D中第1行的元素自左向右依次为－1，
计算三阶行列式： 计算四阶行列式：计算四阶行列式： 请帮忙给出正确答案和分析 谢谢！
计算三阶行列式： 计算四阶行列式：计算四阶行列式： 请帮忙给出正确答案和分析，谢谢！
