有一平底容器 其内侧壁是由曲线x＝ψ(y)(y≥0)绕y轴旋转而成的旋转曲面(如图1—6—1) 容器
有一平底容器，其内侧壁是由曲线x＝ψ(y)(y≥0)绕y轴旋转而成的旋转曲面(如图1—6—1)，容器的底面圆的半径为2m．根据设计要求，当以3m3／min的速率向容器内注入液体时，液面的面积将以πm2／min的速率均匀扩大(假设注入液体前，容器内无液体)．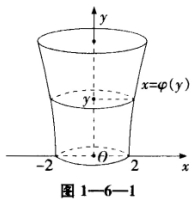 
(1)根据t时刻液面的面积，写出t与ψ(y)之间的关系式； (2)求曲线x＝ψ(y)的方程． (注：m表示长度单位米，min表示时间单位分)
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-09 09:50:03
正确答案：(1)设在t时刻。液面的高度为y则由题设知此时液面的面积为πψ2(y)＝4π＋πt从而t＝ψ2(y)－4． (2)液面的高度为y时液体的体积为π∫0yψ2(u)du＝3t＝3ψ2(y)－12．上式两边对y求导得 πψ2(y)＝6ψ(y)ψ'(y)即 πψ(y)＝6qψ'(y)．解此方程得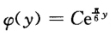 
其中C为任意常数由ψ(0)＝2知C＝2故所求曲线方程为 
．
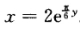[分析液面的面积将以πm2／min的速率均匀扩大，因此t时刻液面面积应为22π＋πt，而液面为圆，其面积可直接计算出来，由此可导出t与ψ(y)之间的关系式；又液体的体积可根据旋转体的体积公式用定积分计算，已知t时刻的液体体积为3t，它们之间也可建立积分关系式，求导后转化为微分方程求解即可．[评注作为应用题，本题比较好地综合考查了定积分在几何上的应用与微分方程的求解．
相似问题
已知某车间的容积为30×30×6m3 车间内空气中CO2的含量为0．12％ 现输入CO2含量为0．0
已知某车间的容积为30×30×6m3，车间内空气中CO2的含量为0．12％，现输入CO2含量为0．04％的新鲜空气，假定新鲜空气进入车间后立即与车间内原有空气均匀
某湖泊的水量为V 每年排人湖泊内含污染物A的污水量为 流入湖泊内不含A的水量为 流出湖泊的水量为．已
某湖泊的水量为V，每年排人湖泊内含污染物A的污水量为，流入湖泊内不含A的水量为，流出湖泊的水量为．已知1999年年底湖中A的含量为5m0，超过国家规定指标
设有一高度为h(t)(t为时间)的雪堆在融化过程中 其侧面满足方程z＝h(t)－(设长度单位为厘米
设有一高度为h(t)(t为时间)的雪堆在融化过程中，其侧面满足方程z＝h(t)－(设长度单位为厘米，时间单位为小时)．已知体积减少的速率与侧面积成正比(比例系
下列结论中正确的是A．都收敛．B．都发散．C．收敛．D．发散．请帮忙给出正确答案和分析 谢谢！
下列结论中正确的是A．都收敛．B．都发散．C．收敛．D．发散．请帮忙给出正确答案和分析，谢谢！
用Γ函数表示下列积分 并指出这些积分的收敛范围。 请帮忙给出正确答案和分析 谢谢！
用Γ函数表示下列积分，并指出这些积分的收敛范围。 请帮忙给出正确答案和分析，谢谢！
