一个质量为m的质点在OXY平面上运动 其位置矢量为r=acosωti+bsinωtj（SI） 式中

正确答案：（1）由速度定义可求出质点在任意一点处的速度具体表示为V=-aωsinωti+bωcosωtj （1）将点C（a0）的坐标代入位置矢量表达式可知cosωt=1sinωt=0将此关系代入式（1）可得到质点在点C的速度为v_c=bωj。同理将D（0b）的坐标代入位置矢量表达式可知cosωt=0sinωt=1将此关系代入式（1）可得到质点在点D的速度为v_D=-aωt。由质点动能的定义可得到质点在点C和点D的动能分别为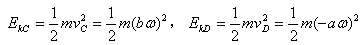 （2）（2）由加速度的定义可得质点的加速度为a=-aω²cosωti-bω²sinωtj （3） 由牛顿运动定律可得质点所受的合外力F为F=ma=-maω²cosωti-mbω²sinωtj由于r=acosωti+bsinωtj则有F=-mω²r由质点的动能定理可得F的分力F_x和F_y所做的功分别为[*4.4
（1）由速度定义,可求出质点在任意一点处的速度,具体表示为V=-aωsinωti+bωcosωtj（1）将点C（a,0）的坐标代入位置矢量表达式可知,cosωt=1,sinωt=0,将此关系代入式（1）,可得到质点在点C的速度为vc=bωj。同理,将D（0,b）的坐标代入位置矢量表达式可知,cosωt=0,sinωt=1,将此关系代入式（1）,可得到质点在点D的速度为vD=-aωt。由质点动能的定义,可得到质点在点C和点D的动能分别为（2）（2）由加速度的定义,可得质点的加速度为a=-aω2cosωti-bω2sinωtj（3）由牛顿运动定律可得质点所受的合外力F为F=ma=-maω2cosωti-mbω2sinωtj由于r=acosωti+bsinωtj,则有F=-mω2r由质点的动能定理,可得F的分力Fx和Fy所做的功分别为[*4.4