考虑下列问题： min x1x2 s．t． g(x)=一2x1+x2+3≥0． (1)用二阶最优性条
考虑下列问题： min x1x2 s．t． g(x)=一2x1+x2+3≥0． (1)用二阶最优性条件证明点 
是局部最优解．并说明它是否为全局最优解? (2)定义障碍函数为 G(x，r)=x1x2一rlng(x)，试用内点法求解此问题，并说明内点法产生的序列趋向点
．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-14 10:54:04
正确答案：(1)在点
目标函数和约束函数的梯度分别是
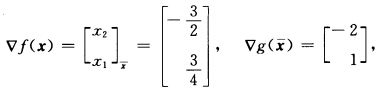g(x)≥0是起作用约束．令
取Lagrange函数 L(xω)=x1x2一ω(一2x1+x2+3)则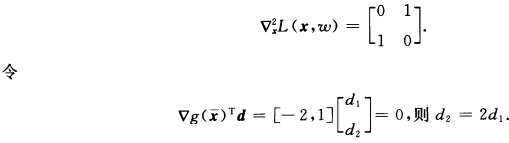
方向集
(2)对于障碍函数 G(xr)=x1x2一rln(一2x1+x2+3)令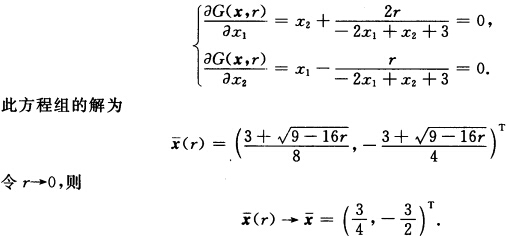
(1)在点,目标函数和约束函数的梯度分别是g(x)≥0是起作用约束．令取Lagrange函数L(x,ω)=x1x2一ω(一2x1+x2+3),则方向集(2)对于障碍函数G(x,r)=x1x2一rln(一2x1+x2+3),令
相似问题
用乘子法求解下列问题： (1)min x12+x22 s．t． x1≥1； (2)min s．t．
用乘子法求解下列问题： (1)min x12+x22 s．t． x1≥1； (2)min s．t．x1≥0， x2≥1请帮忙给出正确答案和分析，谢谢！
热力学系统的状态取决于__________；如果系统的__________全部都有确定值 则系统的_
热力学系统的状态取决于__________；如果系统的__________全部都有确定值，则系统的__________就一定是确定的。请帮忙给出正确答案和分析，谢谢！
C(石墨) C(金刚石) O3(臭氧)都是单质 它们的标准摩尔生成焓都为零。此题为判断题(对 错)。
C(石墨)、C(金刚石)、O3(臭氧)都是单质，它们的标准摩尔生成焓都为零。此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
用既约梯度法求解下列问题：min (x1－2)2＋(x2－2)2 s．t． x1＋x2≤2 x1
用既约梯度法求解下列问题：min (x1－2)2＋(x2－2)2 s．t． x1＋x2≤2， x1，x2≥0， 取初始点xmin (x1-2)2+(x2-2)2 s．t． x1+x2≤2， x1，x2
根据系统与环境之间是否存在物质和能量的交换 可将系统分为三种类型 即__________ _____
根据系统与环境之间是否存在物质和能量的交换，可将系统分为三种类型，即__________、__________和____________。请帮忙给出正确答案和分析，谢谢！
