证明:曲面M:x(x y)=(x y f(x y))的第1 第2基本形式分别为从球面M=S2(R):
证明:曲面M:x(x,y)=(x,y,f(x,y))的第1、第2基本形式分别为从球面M=S2(R):x2+y2+z2=R2的北极向xOy
从球面M=S2(R):x2+y2+z2=R2的北极向xOy平面作球极投影.证明:球面M的第1基本形式为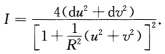
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: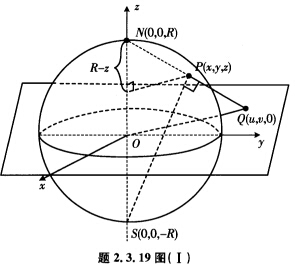 北极投影:由北极N(00R)向平面z=0投影(习题2.3.19图(I)).设P(xyz)∈M=S2(R)直线NP交平面z=0于(uv0).由于相似三角形对应成比例故有
北极投影:由北极N(00R)向平面z=0投影(习题2.3.19图(I)).设P(xyz)∈M=S2(R)直线NP交平面z=0于(uv0).由于相似三角形对应成比例故有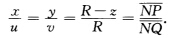 再由△NPS∽△NOQ得到
再由△NPS∽△NOQ得到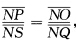
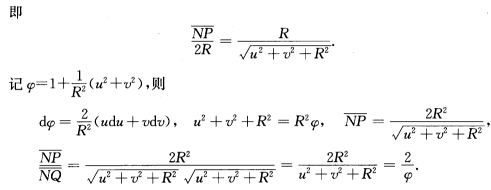 用uv表示球面参数使得(也可参阅[7第9页)x(uv)=(x(uv)y(uv)z(uv))=φ-1(2u2vR(φ~2))dx=φ-1(2du2dvRdφ)一φ2dφ(2u2vR(φ—2))=2φ-1(dudv0)一2φ-2dφ(uv一R)I=dx2=4[φ-1(dudv0)一φ-2dφ(uv一R)2=4φ-2[(dudv0)2+φ-2(dφ)2(uv一R)2一2φ-1dφ(dudv0).(uv一R)=4φ-2[du2+dv2+φ-2(dφ)2(u2+v2+R2)一2φ-1dφ(udu+vdv)
用uv表示球面参数使得(也可参阅[7第9页)x(uv)=(x(uv)y(uv)z(uv))=φ-1(2u2vR(φ~2))dx=φ-1(2du2dvRdφ)一φ2dφ(2u2vR(φ—2))=2φ-1(dudv0)一2φ-2dφ(uv一R)I=dx2=4[φ-1(dudv0)一φ-2dφ(uv一R)2=4φ-2[(dudv0)2+φ-2(dφ)2(uv一R)2一2φ-1dφ(dudv0).(uv一R)=4φ-2[du2+dv2+φ-2(dφ)2(u2+v2+R2)一2φ-1dφ(udu+vdv)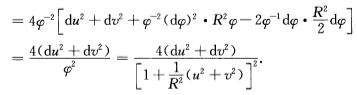
北极投影:由北极N(0,0,R)向平面z=0投影(习题2.3.19图(I)).设P(x,y,z)∈M=S2(R),直线NP交平面z=0于(u,v,0).由于相似三角形对应成比例,故有再由△NPS∽△NOQ,得到用u,v表示球面参数,使得(也可参阅[7第9页)x(u,v)=(x(u,v),y(u,v),z(u,v))=φ-1(2u,2v,R(φ~2)),dx=φ-1(2du,2dv,Rdφ)一φ2dφ(2u,2v,R(φ—2))=2φ-1(du,dv,0)一2φ-2dφ(u,v,一R),I=dx2=4[φ-1(du,dv,0)一φ-2dφ(u,v,一R)2=4φ-2[(du,dv,0)2+φ-2(dφ)2(u,v,一R)2一2φ-1dφ(du,dv,0).(u,v,一R)=4φ-2[du2+dv2+φ-2(dφ)2(u2+v2+R2)一2φ-1dφ(udu+vdv)
相似问题
求圆柱螺线x(t)=(cos t sin t t) (t∈R)的渐缩线y(t).请帮忙给出正确答案和
求圆柱螺线x(t)=(cos t,sin t,t) (t∈R)的渐缩线y(t).请帮忙给出正确答案和分析,谢谢!
抛物线:y=x2 其参数表示为x(t)=(x(t) y(t))=(t t2);请帮忙给出正确答案和分
抛物线:y=x2,其参数表示为x(t)=(x(t),y(t))=(t,t2);请帮忙给出正确答案和分析,谢谢!
用各种方法证明:(1)平面的测地线为直线;(2)圆柱面的测地线为圆柱螺线 直母线 z=常数截圆柱面所
用各种方法证明:(1)平面的测地线为直线;(2)圆柱面的测地线为圆柱螺线、直母线、z=常数截圆柱面所得的圆.请帮忙给出正确答案和分析,谢谢!
R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)满足:则或者x(s)为球面曲线
R3中k≠0,τ≠0的C4连通曲线x(s)为球面曲线等价于如果x(s)满足:则或者x(s)为球面曲线,或者x(s)为常如果x(s)满足:则或者x(s)为球面曲线,或者x(s)为常
设φ(u v)=常数 φ(u v)=常数为曲面M上的两族正则曲线.证明:两族曲线正交Eφvψv一F(
设φ(u,v)=常数,φ(u,v)=常数为曲面M上的两族正则曲线.证明:两族曲线正交Eφvψv一F(φuψv+φvψu)+Gφuψu=0请帮忙给出正确答案和分析,谢谢!












