试证：级数 所定义的函数在左半平面内解析 并可解析延拓到除去点z=0外的整个z平面．请帮忙给出正确
试证：级数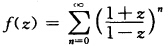 
所定义的函数在左半平面内解析，并可解析延拓到除去点z=0外的整个z平面．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***103
2024-11-21 07:15:13
正确答案：由于fn(z)=
它把Re z=0映射为｜w｜=1；把Re z＜0映射为｜w｜＜1．而级数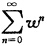
的收敛圆为｜w｜＜1且和函数为
在Re z＜0内为内闭的一致收敛于f(z)=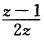
故f(z)在Re z＜0内解析． 又由于
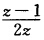在z平面上除z=0外处处解析故f(z)可以解析延拓到除z=0外的整个z平面上．
由于fn(z)=,它把Rez=0映射为｜w｜=1；把Rez＜0映射为｜w｜＜1．而级数的收敛圆为｜w｜＜1,且和函数为在Rez＜0内为内闭的一致收敛于f(z)=,故f(z)在Rez＜0内解析．又由于在z平面上除z=0外,处处解析,故f(z)可以解析延拓到除z=0外的整个z平面上．
相似问题
设袋中装有α只红球 b只白球 每次自袋中任取一只球 观察颜色后放回 并同时再放入m只与所取出的那只同
设袋中装有α只红球，b只白球，每次自袋中任取一只球，观察颜色后放回，并同时再放入m只与所取出的那只同色的球，连续在袋中取球四次，试求第一，二次取
试计算积分 β＞0 b＞0．请帮忙给出正确答案和分析 谢谢！
试计算积分，β＞0，b＞0．请帮忙给出正确答案和分析，谢谢！
试证：若a为f(z)的单值性孤立奇点 则a为f(z)的m阶极点的充要条件是 (含点∞的区域的柯西积分
试证：若a为f(z)的单值性孤立奇点，则a为f(z)的m阶极点的充要条件是 (含点∞的区域的柯西积分(含点∞的区域的柯西积分定理)设C是一条周线，区域D是C的外
试证： 试证：试证：请帮忙给出正确答案和分析 谢谢！
试证： 试证：试证：请帮忙给出正确答案和分析，谢谢！
证明：函数z－2是函数 试证： 互为直接解析延拓．试证： 互为直接解析延拓．请帮忙给出正确答案和分
证明：函数z－2是函数 试证： 互为直接解析延拓．试证： 互为直接解析延拓．请帮忙给出正确答案和分析，谢谢！
