已知三元非齐次线性方程组Aχ＝β(β≠0) 其增广矩阵的秩r()与系数矩阵A的秩r(A)都等于2 且
已知三元非齐次线性方程组Aχ＝β(β≠0)，其增广矩阵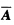
的秩r(
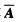)与系数矩阵A的秩r(A)都等于2，且向量η1，η2，η3都是它的解向量，若向量 
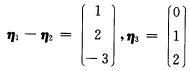则它的全部解为______．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***101
2024-11-13 07:25:10
正确答案：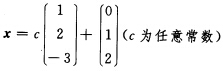
由于增广矩阵的秩r()与系数矩阵A的秩r(A)都等于2，而未知量的个数n＝3，有秩r()＝r(A)＝21，η2都是此非齐次线性方程组Aχ＝β(β≠0)的解向量，从而向量η1－η2，是其导出组Aχ＝0的解向量，它显然是非零向量，因而线性无关，这说明导出组Aχ＝0的一个基础解系当然为η1－η2因此此非齐次线性方程组Aχ＝β(β≠0)的全部解为于是应将直接填在空内．
相似问题
已知五元齐次线性方程组AX＝0 若它仅有零解 则系数矩阵A的秩r(A)＝_______．请帮忙给出正
已知五元齐次线性方程组AX＝0，若它仅有零解，则系数矩阵A的秩r(A)＝_______．请帮忙给出正确答案和分析，谢谢！
已知线性方程组AX＝B有解 若系数矩阵A的秩r(A)＝4 则增广矩阵的秩r()＝______．请帮忙
已知线性方程组AX＝B有解，若系数矩阵A的秩r(A)＝4，则增广矩阵的秩r()＝______．请帮忙给出正确答案和分析，谢谢！
已知非齐次线性方程组Aχ＝β(β≠0) 若向量考是其导出组Aχ＝0的解向量 向量η是它的解向量 则线
已知非齐次线性方程组Aχ＝β(β≠0)，若向量考是其导出组Aχ＝0的解向量，向量η是它的解向量，则线性组合3ξ＋2η是非齐次线性方程组( )的解向量．A．
若线性方程组AX＝B的增广矩阵经初等行变换化为 则当常数λ＝______时 此线性方程组有无穷多解
若线性方程组AX＝B的增广矩阵经初等行变换化为 则当常数λ＝______时，此线性方程组有无穷多解．请帮忙给出正确答案和分析，谢谢！
求下列矩阵与矩阵的积： 求下列方阵的幂：求下列方阵的幂： 请帮忙给出正确答案和分析 谢谢！
求下列矩阵与矩阵的积： 求下列方阵的幂：求下列方阵的幂： 请帮忙给出正确答案和分析，谢谢！
