求微分方程 将下列方程化为可分离变量方程 并求解.将下列方程化为可分离变量方程 并求解. 请帮忙给出
求微分方程 将下列方程化为可分离变量方程,并求解.
将下列方程化为可分离变量方程,并求解. 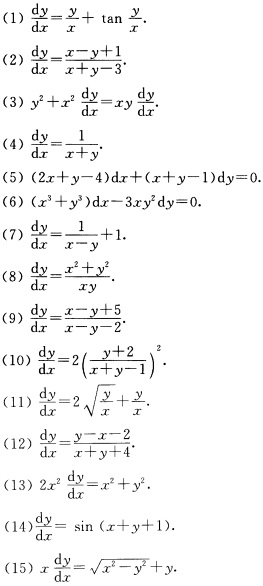
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)令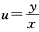 原方程变为
原方程变为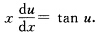 用分离变量法求得其通解为sinu=Cx.其中C为任意常数.将u换成
用分离变量法求得其通解为sinu=Cx.其中C为任意常数.将u换成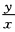 得原方程的通解为
得原方程的通解为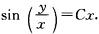 (2)令x=ξ+1y=η+2可将原方程变为
(2)令x=ξ+1y=η+2可将原方程变为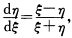 令
令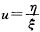 则有
则有 用分离变量法求得其通解为u2+2u-1=C1ξ-2其中C1为任意常数.再由
用分离变量法求得其通解为u2+2u-1=C1ξ-2其中C1为任意常数.再由 代入上式并化简得原方程的通解为y2+2xy-x2一6y一2x=C其中C为任意常数。
代入上式并化简得原方程的通解为y2+2xy-x2一6y一2x=C其中C为任意常数。 用分离变量法求得其通解为u2一4u+14x=C将u换成x-y得原方程的通解为(x—y)2+10x+4y=C其中C为任意常数.(10)令x=ξ+3y=η-2可将原方程变为
用分离变量法求得其通解为u2一4u+14x=C将u换成x-y得原方程的通解为(x—y)2+10x+4y=C其中C为任意常数.(10)令x=ξ+3y=η-2可将原方程变为 令
令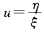 则有
则有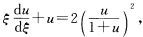 用分离变量法求得其通解为In|uξ|+2arctanu=C及u=0其中C为任意常数.再由
用分离变量法求得其通解为In|uξ|+2arctanu=C及u=0其中C为任意常数.再由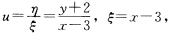 代入上式并化简得原方程的通解为
代入上式并化简得原方程的通解为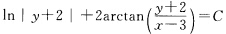 及y=一2.(11)令
及y=一2.(11)令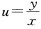 原方程变为
原方程变为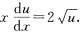 用分离变量法求得其解为u=(In|x|+C)2及u=0其中C为任意常数.将u换成
用分离变量法求得其解为u=(In|x|+C)2及u=0其中C为任意常数.将u换成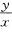 得原方程的解为y=x(In|x|+C)2及y=0(x≠0).(12)令x=ξ一3y=η-1可将原方程变为
得原方程的解为y=x(In|x|+C)2及y=0(x≠0).(12)令x=ξ一3y=η-1可将原方程变为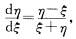 令
令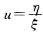 则有
则有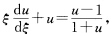
 当1+sinu≠0时用分离变量法求得其通解为tanu-secu=x+C将u换成x+y+1得原方程的通解为 tan(x+y+1)一sec(x+y+1)=x+C其中C为任意常数.此外由1+sinu=0可得原方程还有解
当1+sinu≠0时用分离变量法求得其通解为tanu-secu=x+C将u换成x+y+1得原方程的通解为 tan(x+y+1)一sec(x+y+1)=x+C其中C为任意常数.此外由1+sinu=0可得原方程还有解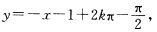 其中k为任意整数.(15)若x>0将原方程改写为
其中k为任意整数.(15)若x>0将原方程改写为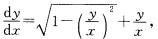 令
令 则有
则有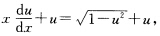 当u2一1≠0时用分离变量法求得其通解为u=sin(Inx+C)将u换成
当u2一1≠0时用分离变量法求得其通解为u=sin(Inx+C)将u换成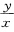 得y=xsin(Inx+C);又由u2一1=0可得原方程还有解y2=x2.对x<0可类似讨论最后得原方程的通解为y=|x|sin(In|x|+C)并且y2=x2也是方程的解其中C为任意常数.
得y=xsin(Inx+C);又由u2一1=0可得原方程还有解y2=x2.对x<0可类似讨论最后得原方程的通解为y=|x|sin(In|x|+C)并且y2=x2也是方程的解其中C为任意常数.
(1)令,原方程变为用分离变量法求得其通解为sinu=Cx.其中C为任意常数.将u换成得原方程的通解为(2)令x=ξ+1,y=η+2,可将原方程变为令,则有用分离变量法求得其通解为u2+2u-1=C1ξ-2,其中C1为任意常数.再由代入上式并化简得原方程的通解为y2+2xy-x2一6y一2x=C,其中C为任意常数。用分离变量法求得其通解为u2一4u+14x=C,将u换成x-y得原方程的通解为(x—y)2+10x+4y=C,其中C为任意常数.(10)令x=ξ+3,y=η-2,可将原方程变为令,则有用分离变量法求得其通解为In|uξ|+2arctanu=C及u=0,其中C为任意常数.再由代入上式并化简得原方程的通解为及y=一2.(11)令,原方程变为用分离变量法求得其解为u=(In|x|+C)2及u=0,其中C为任意常数.将u换成得原方程的解为y=x(In|x|+C)2及y=0(x≠0).(12)令x=ξ一3,y=η-1,可将原方程变为令,则有当1+sinu≠0时用分离变量法求得其通解为tanu-secu=x+C,将u换成x+y+1得原方程的通解为tan(x+y+1)一sec(x+y+1)=x+C,其中C为任意常数.此外由1+sinu=0可得原方程还有解其中k为任意整数.(15)若x>0,将原方程改写为令,则有当u2一1≠0时,用分离变量法求得其通解为u=sin(Inx+C),将u换成得y=xsin(Inx+C);又由u2一1=0可得原方程还有解y2=x2.对x<0可类似讨论,最后得原方程的通解为y=|x|sin(In|x|+C),并且y2=x2也是方程的解,其中C为任意常数.
相似问题
(89年考研题)若齐次线性方程组位于第k个位置的数n作成多少个逆序?位于第k个位置的数n作成多少个逆
(89年考研题)若齐次线性方程组位于第k个位置的数n作成多少个逆序?位于第k个位置的数n作成多少个逆序?请帮忙给出正确答案和分析,谢谢!
总量指标数值随总体范围大小而改变。( )此题为判断题(对 错)。请帮忙给出正确答案和分析 谢谢!
总量指标数值随总体范围大小而改变。( )此题为判断题(对,错)。请帮忙给出正确答案和分析,谢谢!
验证 如果齐次方程组有一个相同的基解矩阵 证明:A1(t)≡A2(t).如果齐次方程组有一个相同的基
验证 如果齐次方程组有一个相同的基解矩阵,证明:A1(t)≡A2(t).如果齐次方程组有一个相同的基解矩阵,证明:A1(t)≡A2(t).请帮忙给出正确答案和分析,谢谢!
试求初值问题 的Picard迭代序列 并通过求迭代序列的极限求出初值问题的解 这里P(t) Q(t
试求初值问题 的Picard迭代序列,并通过求迭代序列的极限求出初值问题的解,这里P(t),Q(t)均为连续函数.请帮忙给出正确答案和分析,谢谢!
证明若xs(t)(s=1 2 … m)分别是方程 用幂级数法求方程 满足初值条件x(1)=7 x(1
证明若xs(t)(s=1,2,…,m)分别是方程 用幂级数法求方程 满足初值条件x(1)=7,x(1)=3的解.用幂级数法求方程 满足初值条件x(1)=7,x(1)=3的解.请












