求微分方程y'(zx+y2)=y满足初始条件y(1)=y(1)=1的特解.请帮忙给出正确答案和分析
求微分方程y"(zx+y2)=y满足初始条件y(1)=y(1)=1的特解.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:令y'=u则原方程化为 u'(x+u2)=u.即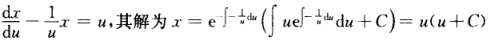 利用u=y'(1)=1有C=0于是x=u2或[1890*代入初始条件y(1)=1得
利用u=y'(1)=1有C=0于是x=u2或[1890*代入初始条件y(1)=1得 故满足初始条件y(1)=y'(1)=1的特解为
故满足初始条件y(1)=y'(1)=1的特解为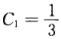 。
。
本题为可降阶的二阶微分方程,作变量代换即可.
相似问题
设f(x) g(x)都是[a b]上的连续函数 且g(x)在[a b]上不变号 证明:至少存在一点ε
设f(x),g(x)都是[a,b]上的连续函数,且g(x)在[a,b]上不变号,证明:至少存在一点ε∈[a,b],使得下式成立 请帮忙给出正确答案和分析,谢谢!
设位于第一象限的曲线y=f(x)过点 其上任一点P(x y)处的法线与y轴的交点为Q 且线段PQ被x
设位于第一象限的曲线y=f(x)过点,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分. (1)求曲线y=f(x)的方程; (2)已知曲线y=sinx在[0
试求a b的值 使得由曲线y=cosx(0≤x≤π/2)与两坐标轴所围成的图形的面积被曲线y=asi
试求a,b的值,使得由曲线y=cosx(0≤x≤π/2)与两坐标轴所围成的图形的面积被曲线y=asinx与y=bsinx三等分.请帮忙给出正确答案和分析,谢谢!
一物体按规律x=a3作直线运动 媒质的阻力与速度的平方成正比.计算物体由x=0移至x=a时 克服媒质
一物体按规律x=a3作直线运动,媒质的阻力与速度的平方成正比.计算物体由x=0移至x=a时,克服媒质阻力所作的功.请帮忙给出正确答案和分析,谢谢!
利用定积分定义计算由抛物线y=x2+1 两直线x=a x=b(b>a)及x轴所围成图形的面积.请帮忙
利用定积分定义计算由抛物线y=x2+1,两直线x=a,x=b(b>a)及x轴所围成图形的面积.请帮忙给出正确答案和分析,谢谢!












