设位于第一象限的曲线y=f(x)过点 其上任一点P(x y)处的法线与y轴的交点为Q 且线段PQ被x
设位于第一象限的曲线y=f(x)过点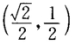 ,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分. (1)求曲线y=f(x)的方程; (2)已知曲线y=sinx在[0,π]上的弧长为l,试用,表示曲线y=f(x)的弧长s.
,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分. (1)求曲线y=f(x)的方程; (2)已知曲线y=sinx在[0,π]上的弧长为l,试用,表示曲线y=f(x)的弧长s.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)曲线y=f(x)在点尸(xy)处的法线方程为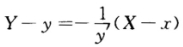 其中(XY)为法线上任意一点的坐标.令X=0则
其中(XY)为法线上任意一点的坐标.令X=0则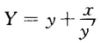 故Q点的坐标为
故Q点的坐标为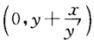 .由题设知
.由题设知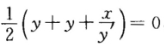 即2ydy+xdx=0.积分得 x2+2y2=C(C为任意常数).由
即2ydy+xdx=0.积分得 x2+2y2=C(C为任意常数).由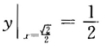 知C=1故曲线y=f(x)的方程为 x2+2y2=1.(2)曲线y=sinx在[0π上的弧长为
知C=1故曲线y=f(x)的方程为 x2+2y2=1.(2)曲线y=sinx在[0π上的弧长为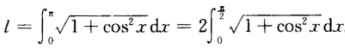 曲线y=f(x)的参数方程为
曲线y=f(x)的参数方程为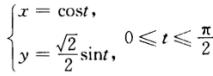 故
故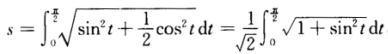 令
令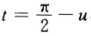 则
则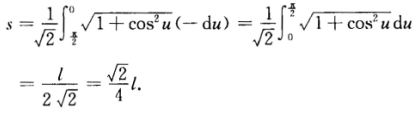
[分析(1)先求出法线方程与交点坐标Q,再由题设线段PQ被x轴平分,可转化为微分方程,求解此微分方程即可得曲线y=f(x)的方程.(2)将曲线y=f(x)化为参数方程,再利用弧长公式进行计算即可.[评注注意:只在第一象限考虑曲线y=f(x)的弧长,所以积分限应从0到,而不是从0到2π.
相似问题
试求a b的值 使得由曲线y=cosx(0≤x≤π/2)与两坐标轴所围成的图形的面积被曲线y=asi
试求a,b的值,使得由曲线y=cosx(0≤x≤π/2)与两坐标轴所围成的图形的面积被曲线y=asinx与y=bsinx三等分.请帮忙给出正确答案和分析,谢谢!
一物体按规律x=a3作直线运动 媒质的阻力与速度的平方成正比.计算物体由x=0移至x=a时 克服媒质
一物体按规律x=a3作直线运动,媒质的阻力与速度的平方成正比.计算物体由x=0移至x=a时,克服媒质阻力所作的功.请帮忙给出正确答案和分析,谢谢!
利用定积分定义计算由抛物线y=x2+1 两直线x=a x=b(b>a)及x轴所围成图形的面积.请帮忙
利用定积分定义计算由抛物线y=x2+1,两直线x=a,x=b(b>a)及x轴所围成图形的面积.请帮忙给出正确答案和分析,谢谢!
计算下列定积分: 请帮忙给出正确答案和分析 谢谢!
计算下列定积分: 请帮忙给出正确答案和分析,谢谢!
具有特解y1=e-x y2=2xe-x y3=3ex的三阶常系数齐次线性微分方程是A.y'''-y'
具有特解y1=e-x,y2=2xe-x,y3=3ex的三阶常系数齐次线性微分方程是A.y"""-y"—y"+y=0.B.y"""+y"—y"-y=0.C.y"""-6y"+11y"-6y=0.D.












