求微分方程xdy+(x-2y)dx=0的一个解y=y(x) 使得由曲线y=y(x)与直线x=1 x=
求微分方程xdy+(x-2y)dx=0的一个解y=y(x),使得由曲线y=y(x)与直线x=1,x=2以及x轴所围成的平面图形绕x轴旋转一周的旋转体体积最小.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:原方程为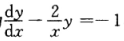 则
则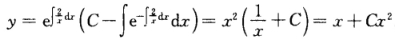 所求旋转体的体积为
所求旋转体的体积为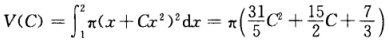 令
令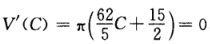 得唯一驻点
得唯一驻点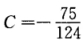 又
又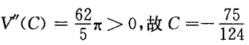 为最小值点于是所求曲线方程为
为最小值点于是所求曲线方程为
原方程为,则所求旋转体的体积为令,得唯一驻点又为最小值点,于是所求曲线方程为
相似问题
设函数f(f)在[0 +∞)上连续 且满足方程 求f(t).请帮忙给出正确答案和分析 谢谢!
设函数f(f)在[0,+∞)上连续,且满足方程,求f(t).请帮忙给出正确答案和分析,谢谢!
由实验知道 弹簧在拉伸过程中 拉力与弹簧的伸长量成正比 已知弹簧拉1cm需要的力是3N 如果把弹簧拉
由实验知道,弹簧在拉伸过程中,拉力与弹簧的伸长量成正比,已知弹簧拉1cm需要的力是3N,如果把弹簧拉伸3cm,计算要作的功.请帮忙给出正确答案和分析,谢谢!
用铁锤将一铁钉击人木板 设木板对铁钉的阻力与铁钉击人木板的深度成正比.在击第一次时 将铁钉击入木板1
用铁锤将一铁钉击人木板,设木板对铁钉的阻力与铁钉击人木板的深度成正比.在击第一次时,将铁钉击入木板1 cm如果铁锤每次打击铁钉所作的功相等,问铁锤
设f(u v)具有连续偏导数 且满足f(u v)+f(u v)=uv.求y(x)=e-2xf(x x
设f(u,v)具有连续偏导数,且满足f(u,v)+f(u,v)=uv.求y(x)=e-2xf(x,x)所满足的一阶微分方程,并求其通解.请帮忙给出正确答案和分析,谢谢!
用变量代换x=cost(0<t<π)化简微分方程(1-x2)y'-xy+y=0 并求其满足的特解.请
用变量代换x=cost(0<t<π)化简微分方程(1-x2)y "-xy+y=0,并求其满足的特解.请帮忙给出正确答案和分析,谢谢!












