已知一个线性移不变因果系统 用如下差分方程描述 y(n)=y(n一1)+y(n一2)+x(n一1)

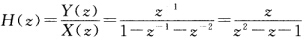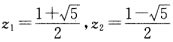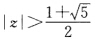正确答案：(1)y(n)=y(n一1)+y(n一2)+x(n—1) 将上式进行Z变换得 Y(z)=z^一1Y(z)+z^一2Y(z)+z^一1X(z)因此零点z=0令z²一z一1=0求出极点：如图2．8所示。 (2)已知系统是因果系统因此收敛域应该选包含∞点在内的区域即利用留数法求系统的冲激响应h(n)即 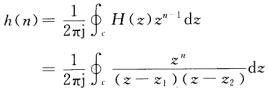当n≥0时有 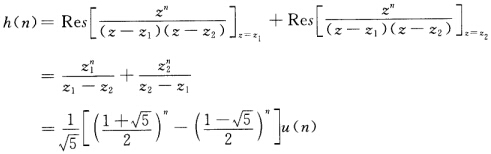(3)如果系统是稳定系统收敛域需选包含单位圆在内的收敛域即∣z₂∣＜∣z∣＜∣z₁∣当n≥0时c内只有极点z₂只需求z₂点的留数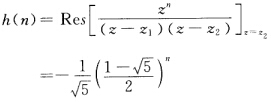当n＜0时c内有两个极点z₂和0因为z=0是一个n阶极点改成求网外极点留数圆外极点只有一个即z₁那么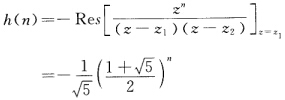最后得到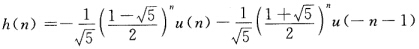
(1)y(n)=y(n一1)+y(n一2)+x(n—1)将上式进行Z变换,得Y(z)=z一1Y(z)+z一2Y(z)+z一1X(z)因此零点z=0,令z2一z一1=0,求出极点：,如图2．8所示。(2)已知系统是因果系统,因此收敛域应该选包含∞点在内的区域,即利用留数法求系统的冲激响应h(n),即当n≥0时,有(3)如果系统是稳定系统,收敛域需选包含单位圆在内的收敛域,即∣z2∣＜∣z∣＜∣z1∣当n≥0时,c内只有极点z2,只需求z2点的留数当n＜0时,c内有两个极点z2和0,因为z=0是一个n阶极点,改成求网外极点留数,圆外极点只有一个,即z1,那么最后得到