试用Gauss—Jordan消去法求下列矩阵的逆矩阵。 设线性方程组为 试分别用平方根法和改进的C设
试用Gauss—Jordan消去法求下列矩阵的逆矩阵。 设线性方程组为 试分别用平方根法和改进的C
设线性方程组为 
试分别用平方根法和改进的Cholesky方法解之。
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-17 09:33:41
正确答案：对方程的系数矩阵A进行Cholesky分解A＝LLT可得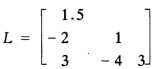
解Ly＝b得y＝(013)T解LTχ＝y得χ＝(231)T。 对方程的系数矩阵A进行改进的Cholesky分解A＝LDLT可得
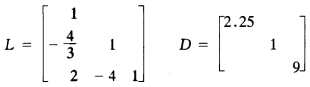解Ly＝b得y＝(019)T解LT＝D-1y得χ＝(231)T。
对方程的系数矩阵A进行Cholesky分解A＝LLT可得解Ly＝b,得y＝(0,1,3)T,解LTχ＝y,得χ＝(2,3,1)T。对方程的系数矩阵A进行改进的Cholesky分解A＝LDLT可得解Ly＝b,得y＝(0,1,9)T,解LT＝D-1y,得χ＝(2,3,1)T。
相似问题
测定试样中MgO的质量百分数 称取试样0．8080g 滴定时消耗了EDTA标准溶液20．50mL 正
测定试样中MgO的质量百分数，称取试样0．8080g，滴定时消耗了EDTA标准溶液20．50mL，正确的测定结果是( )。A．10％B．10 1％C．10 08％D．10 077％请帮
试用n＝1 2 3 4的Newton-cotes求积公式计算定积分I＝请帮忙给出正确答案和分析 谢谢
试用n＝1，2，3，4的Newton-cotes求积公式计算定积分I＝请帮忙给出正确答案和分析，谢谢！
一水样可能含有CO32- OH- HCO3-或者是其混合水样 以酚酞为指示剂。用去10．00mL 0
一水样可能含有CO32-、OH-、HCO3-或者是其混合水样，以酚酞为指示剂。用去10．00mL 0．1000mol／L HCl溶液可滴至终点。问 (1)若水样中含有OH-和CO3一
用0．1025mol·L-1NaOH标准溶液滴定0．4403g邻苯二甲酸氢钾(KHP)样品 用去Na
用0．1025mol·L-1NaOH标准溶液滴定0．4403g邻苯二甲酸氢钾(KHP)样品，用去NaOH溶液20．10mL，计算样品中含KHP的质量。[MKHP＝204．22]请帮忙给出正确答案和分析，谢谢！
一组质量百分数的测定数据为25．01％ 25．03％ 25．04％ 25．05 ％ 计算(1)平均值
一组质量百分数的测定数据为25．01％，25．03％，25．04％，25．05 ％，计算(1)平均值；(2)中位值；(3)平均偏差；(4)相对平均偏差；(5)极差；(6)相对极
