已知齐次线性方程组 已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系; (2)若已知齐
已知齐次线性方程组 已知齐次线性方程组 (1)判别此齐次线性方程组是否存在基础解系; (2)若
已知齐次线性方程组 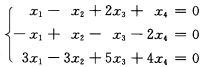 (1)判别此齐次线性方程组是否存在基础解系; (2)若此齐次线性方程组存在基础解系,则求它的一个基础解系.
(1)判别此齐次线性方程组是否存在基础解系; (2)若此齐次线性方程组存在基础解系,则求它的一个基础解系.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)由于齐次线性方程式的个数少于未知量的个数即 m=3 容易看出系数矩阵A的铁r(A)=2而未知量的个数n=4因而基数解系含n-r(A)=4-2=2个线性无关解向量.对所得阶梯形矩阵继续作初等行变换化为简化阶梯形矩阵有
容易看出系数矩阵A的铁r(A)=2而未知量的个数n=4因而基数解系含n-r(A)=4-2=2个线性无关解向量.对所得阶梯形矩阵继续作初等行变换化为简化阶梯形矩阵有 选择未知量χ2χ4为自由未知量未知量χ1χ3为非自由未知量非自由未知量χ1χ3用自由未知量χ2χ4表示其表达式为
选择未知量χ2χ4为自由未知量未知量χ1χ3为非自由未知量非自由未知量χ1χ3用自由未知量χ2χ4表示其表达式为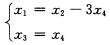 自由未知量χ2取任意常数c1自由未知量4取任意常数c2于是此齐次线性方程组无穷多解的一般表达式为
自由未知量χ2取任意常数c1自由未知量4取任意常数c2于是此齐次线性方程组无穷多解的一般表达式为 再将它写成向量的形式得到解向量的一般表达式即全部解为
再将它写成向量的形式得到解向量的一般表达式即全部解为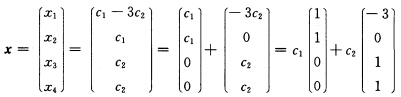 所以此齐次线性方程组的一个基础解系为
所以此齐次线性方程组的一个基础解系为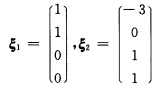
(1)由于齐次线性方程式的个数少于未知量的个数,即m=3作初等行变换,化为阶梯形矩阵,有容易看出,系数矩阵A的铁r(A)=2,而未知量的个数n=4,因而基数解系含n-r(A)=4-2=2个线性无关解向量.对所得阶梯形矩阵继续作初等行变换,化为简化阶梯形矩阵,有选择未知量χ2,χ4为自由未知量,未知量χ1,χ3为非自由未知量,非自由未知量χ1,χ3用自由未知量χ2,χ4表示,其表达式为自由未知量χ2取任意常数c1,自由未知量4取任意常数c2,于是此齐次线性方程组无穷多解的一般表达式为再将它写成向量的形式,得到解向量的一般表达式即全部解为所以此齐次线性方程组的一个基础解系为
相似问题
已知三阶方阵 已知三阶方阵 (1)判别三阶方阵A是否可逆? (2)若三阶方阵A可逆 则求逆矩阵A-1
已知三阶方阵 已知三阶方阵 (1)判别三阶方阵A是否可逆? (2)若三阶方阵A可逆,则求逆矩阵A-1.已知三阶方阵 (1)判别三阶方阵A是否可逆? (2)若三阶
已知向量 若数k使得关系式kα+2β=γ成立 则数k=( ).A.1B.2C.3D.4请帮忙给出正
已知向量 若数k使得关系式kα+2β=γ成立,则数k=( ).A.1B.2C.3D.4请帮忙给出正确答案和分析,谢谢!
已知向量组 已知向量组 (1)判别向量组α1 α2 α3 α4的线性相关性; (2)判别部分组α1
已知向量组 已知向量组 (1)判别向量组α1,α2,α3,α4的线性相关性; (2)判别部分组α1,α2,α3的线已知向量组 (1)判别向量组α1,α2,α3,
若四阶行列式D中第4行的元素自左向右依次为1 2 0 0 余子式M41=2 M42=3 则四阶行列式
若四阶行列式D中第4行的元素自左向右依次为1,2,0,0,余子式M41=2,M42=3,则四阶行列式D=( ).A.-8B.8C.-4D.4请帮忙给出正确答案和分析,谢谢!
计算四阶行列式.请帮忙给出正确答案和分析 谢谢!
计算四阶行列式 请帮忙给出正确答案和分析,谢谢!












