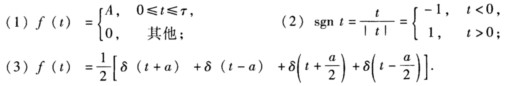参考解答
420***101
2024-11-14 18:06:36
正确答案：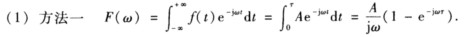
方法二 考虑f(t)=A[u(t)－u(t－τ)从而利用傅氏变换的线性性质也可以很容易得到结果． 
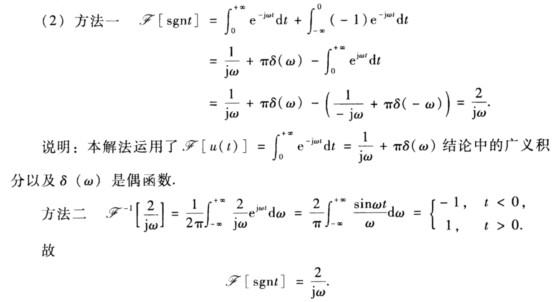说明：本解法运用了“f(t)与F((ω)是一一对应的”。 
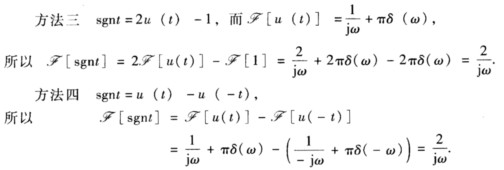(3)方法一 
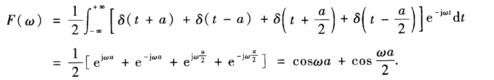方法二直接利用线性性质．
方法二考虑f(t)=A[u(t)－u(t－τ),从而利用傅氏变换的线性性质也可以很容易得到结果．说明：本解法运用了“f(t)与F((ω)是一一对应的”。(3)方法一方法二直接利用线性性质．
相似问题
求下列幂级数的收敛半径 求下列幂级数的和函数求下列幂级数的和函数 请帮忙给出正确答案和分析 谢谢！
求下列幂级数的收敛半径 求下列幂级数的和函数求下列幂级数的和函数 请帮忙给出正确答案和分析，谢谢！
利用卷积定理 证明：请帮忙给出正确答案和分析 谢谢！
利用卷积定理，证明：请帮忙给出正确答案和分析，谢谢！
求下列幂级数的收敛半径 将函数展开为洛朗级数 圆环域为 (1)0
求下列幂级数的收敛半径 将函数展开为洛朗级数，圆环域为 (1)0<|z－i|＜1；(2)1＜|z－i|＜将函数展开为洛朗级数，圆环域为 (1)0<|z－i|＜1；(2)1＜|z
考虑对应下表的运输问题： (1)用西北角法求一初始基本可行解； (2)由(1)中求得的基本可行解出
考虑对应下表的运输问题： (1)用西北角法求一初始基本可行解； (2)由(1)中求得的基本可行解出发，用表上作业法求最优解，使总运输费用最小．请帮忙给
假设给定一个线性规划问题及其一个基本可行解．在此线性规划中 变量之和的上界为σ 在已知的基本可行解处
假设给定一个线性规划问题及其一个基本可行解．在此线性规划中，变量之和的上界为σ，在已知的基本可行解处，目标函数值为f，最大判别数是zk一ck，又设目
