已知f(x)是连续函数 证明:求由曲线y=ex y=e-x与直线x=1所围图形的面积.求由曲线y=e
已知f(x)是连续函数,证明:求由曲线y=ex,y=e-x与直线x=1所围图形的面积.
求由曲线y=ex,y=e-x与直线x=1所围图形的面积.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:曲线y=ex与y=e-x交于点(01).所求面积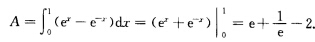
曲线y=ex与y=e-x交于点(0,1).所求面积
相似问题
函数在区间上 曲线y=sinx与直线y=0所围成的图形.在区间上 曲线y=sinx与直线y=0所围
函数在区间上,曲线y=sinx与直线y=0所围成的图形.在区间上,曲线y=sinx与直线y=0所围成的图形. 请帮忙给出正确答案和分析,谢谢!
已知三阶行列式计算行列式计算行列式请帮忙给出正确答案和分析 谢谢!
已知三阶行列式计算行列式计算行列式请帮忙给出正确答案和分析,谢谢!
验证函数x=C1coskt+C2sinkt是微分方程求函数所满足的一阶微分方程 并指出其是否是线性微
验证函数x=C1coskt+C2sinkt是微分方程求函数所满足的一阶微分方程,并指出其是否是线性微分方程.求函数所满足的一阶微分方程,并指出其是否是线性微分
求下列微分方程的通解:请帮忙给出正确答案和分析 谢谢!
求下列微分方程的通解:请帮忙给出正确答案和分析,谢谢!
求下列函数的二阶导数:y=e3x-2.y=e3x-2.请帮忙给出正确答案和分析 谢谢!
求下列函数的二阶导数:y=e3x-2.y=e3x-2.请帮忙给出正确答案和分析,谢谢!












