设二次型F(x1 x2 x3)＝ax12＋ax22＋(a－1)x32＋2x1x3—2x2x3． (1

正确答案：(1)二次型f的矩阵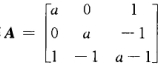由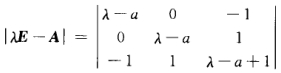＝(λ－a)(λ—a＋2)(λ－a－1)得A的特征值为λ₁＝a－2λ₂＝aλ₃＝a＋1．(2)方法一 由f的规范形为y₁²＋y₂²知A有2个特征值为正1个为零．若λ₁＝a－2＝0即a＝2 则λ₂＝2λ₃＝3符合题意．若λ₂＝a＝0 则λ₁＝－2λ₃＝1不合题意．若λ₃＝a＋1＝0即a＝－1 则λ₁＝－3λ₂＝－1不合题意．综上所述a＝2．方法二 由f的规范形为y₁²＋y₂²知A有合同矩阵其秩为2故｜A｜＝λ₁λ₂λ₃＝0于是a＝2或a＝0或a＝－1．当a＝2时λ₁＝0λ₂＝2λ₃＝3符合题意．当a＝0时λ₁＝－2λ₂＝0λ₃＝1不合题意．当a＝－1时λ₁＝－3λ₂＝－1λ₃＝0不合题意．综上所述a＝2．方法三 由f的规范形为y₁²＋y₂²知A有2个特征值为正1个为零． 显然a－2＜a＜a＋1所以a＝2．
本题已知规范形反求参数，实际上相当于告诉了正负惯性指数，而正负惯性指数又可以通过正负特征值进行确定．