设有3维列向量 确定常数a 使向量组α1＝(1 1 a) α2＝(1 a 1) α3一(a 1 1)

正确答案：对矩阵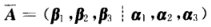作初等行变换有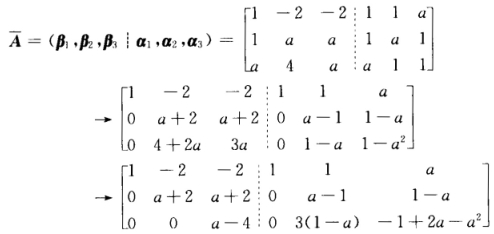当a＝－2时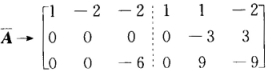显然α₂不能由β₁β₂β₃线性表示因此a≠－2； 当a＝4时显然α₂α₃均不能由β₁β₂β₃线性表示因此a≠4． 而当a≠－2且a≠4时r(β₁β₂β₃)＝3此时向量组α₁α₂α₃可由向量组β₁β₂β₃线性表示．又由题设向量组β₁β₂β₃不能由向量组α₁α₂α₃线性表示必有a－1＝0或2－a－a²＝0即a＝1或a＝－2． 综上所述满足题设条件的只能是a＝1．
[分析向量组α1，α2，α3可由向量组β1，β2，β3线性表示，相当于方程组：αi＝x1β1，x2β2，x3β3，i＝1，2，3．均有解，问题转化为r(β1，β2，β3)＝r(β1，β2，β3)，i＝1，2，3是否均成立?这通过初等变换化阶梯形讨论即可．而向量组β1，β2，β3不能由向量组β1，β2，β3线性表示，相当于至少有一个向量β(j＝1，2，3)不能由α1，α2，α3线性表示，即至少有一方程组βi＝x1α1，x2α2，x3α3，j＝1，2，3，无解．[评注1向量组β1，β2，β3不能由向量组α1，α2，α3线性表示，必有行列式｜[α1，α2，α3｜＝0，由此也可确定a．[评注2向量组能否线性表示的问题完全转化为线性方程组是否有解的问题．