由质量为M的木块和劲度系数为k的轻质弹簧组成在光滑水平台上运动的谐振子 如图6-2所示．开始时木块静
由质量为M的木块和劲度系数为k的轻质弹簧组成在光滑水平台上运动的谐振子，如图6-2所示．开始时木块静止在点O．一颗质量为m的子弹以速率v0。沿水平方向射入木块并嵌在其中，然后木块(内有子弹)做简谐振动．若从子弹射入木块并嵌在木块中时开始计时，试写出系统的振动方程(选取X轴如图6-2所示)．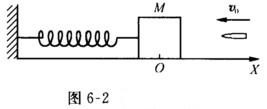 
分析 子弹和木块作完全非弹性碰撞后，子弹、木块和弹簧组成的系统做简谐振动．求系统的振动方程，关键是要求出ω，A，φ．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***100
2024-11-03 23:08:12
正确答案：子弹、木块和弹簧组成的弹簧振子系统的角频率为
子弹与木块碰撞的过程动量守恒．设它们碰撞后的共同速度为v则 mv0=(M+m)v (2)由式(2)解得
子弹和木块碰撞后从平衡位置开始运动初始位置为x0=0初始速度为v它也是振动的最大速度vm．因为vm=ωA所以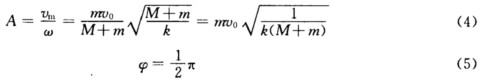
系统的振动方程为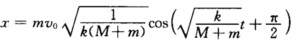
子弹、木块和弹簧组成的弹簧振子系统的角频率为子弹与木块碰撞的过程动量守恒．设它们碰撞后的共同速度为v,则mv0=(M+m)v(2)由式(2)解得子弹和木块碰撞后从平衡位置开始运动,初始位置为x0=0,初始速度为v,它也是振动的最大速度vm．因为vm=ωA,所以系统的振动方程为
相似问题
两个同方向 同频率的简谐振动分别可表示为x1=0.60cos(8πt-3π/4) x2=0.90co
两个同方向、同频率的简谐振动分别可表示为x1=0 60cos(8πt-3π 4)，x2=0 90cos(8πt-π 4)（SI）。（1）求合振动的振幅；（2）另有一个同方向的简谐振动
一根柔绳长为ι 质量为m．绳的一部分在桌面上 其余长度为b的部分从桌面上悬下 如图4-2(a)所示．
一根柔绳长为ι，质量为m．绳的一部分在桌面上，其余长度为b的部分从桌面上悬下，如图4-2(a)所示．设绳与桌面之间的摩擦系数为μ，求：柔绳全部滑离桌面
一根质量为M 长度为ι的链条 被竖直地挂起来 其最低端刚好与秤盘接触．今将链条释放并让它落到秤盘上
一根质量为M、长度为ι的链条，被竖直地挂起来，其最低端刚好与秤盘接触．今将链条释放并让它落到秤盘上，如图3-5所示．求链条的下落长度为x时，秤的读数
花样滑冰运动员绕通过自身的竖直轴转动．开始时两臂伸开 转动惯量为I0 角速度为ω0．然后她将两臂收回
花样滑冰运动员绕通过自身的竖直轴转动．开始时两臂伸开，转动惯量为I0，角速度为ω0．然后她将两臂收回，使转动惯量减少到I0／3．这时她转动的角速度变
一个作直线运动的物体 其速度v与时间t的关系曲线如图4-5所示．设时刻t1至t2间外力做功为A1；时
一个作直线运动的物体，其速度v与时间t的关系曲线如图4-5所示．设时刻t1至t2间外力做功为A1；时刻t2至t3间外力做功为A2；时刻t3至t4间外力做功为A3，则（
