若线性方程组AX＝B的增广矩阵经初等行变换化为 其中λ为常数 则此线性方程组( )．A．可能有无穷
若线性方程组AX＝B的增广矩阵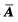
经初等行变换化为 
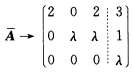其中λ为常数，则此线性方程组( )．
A．可能有无穷多解
B．一定有无穷多解
C．可能无解
D．一定无解
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-13 04:12:54
正确答案：D
注意到增广矩阵经初等行变换已经化为阶梯形矩阵．当常数λ＝0时，秩r()＝2，秩r(A)＝1，由于秩r()≠r(A)，因而此线性方程组无解；当常数λ≠0时，秩r()＝3，秩r(A)＝2，由于秩r()≠r(A)，因而此线性方程组无解．综合上述讨论可知，此线性方程组一定无解．这个正确答案恰好就是备选答案D，所以选择D．
相似问题
若矩阵若n阶方阵A的行列式｜A｜＝2 n阶方阵B的行列式｜B｜＝4 则积AB的行列式｜AB｜＝___
若矩阵若n阶方阵A的行列式｜A｜＝2，n阶方阵B的行列式｜B｜＝4，则积AB的行列式｜AB｜＝______若n阶方阵A的行列式｜A｜＝2，n阶方阵B的行列式｜B｜＝4，
计算三阶行列式： 计算三阶行列式：计算三阶行列式： 请帮忙给出正确答案和分析 谢谢！
计算三阶行列式： 计算三阶行列式：计算三阶行列式： 请帮忙给出正确答案和分析，谢谢！
齐次线性方程组 的解为______．请帮忙给出正确答案和分析 谢谢！
齐次线性方程组 的解为______．请帮忙给出正确答案和分析，谢谢！
计算四阶行列式已知齐次线性方程组 判别它有无非零解．已知齐次线性方程组 判别它有无非零解．请帮忙给
计算四阶行列式已知齐次线性方程组 判别它有无非零解．已知齐次线性方程组 判别它有无非零解．请帮忙给出正确答案和分析，谢谢！
已知矩阵已知二阶方阵 (1)判别二阶方阵A是否可逆? (2)若二阶方阵A可逆 则求逆矩阵A－1．已知
已知矩阵已知二阶方阵 (1)判别二阶方阵A是否可逆? (2)若二阶方阵A可逆，则求逆矩阵A－1．已知二阶方阵 (1)判别二阶方阵A是否可逆? (2)若二阶方阵A
