若数列{xn}满足条件x1=3 xn+1=(x2n+1)/2xn 则该数列的通项公式xn=____

参考解答

467***640

2024-03-17 13:57:45



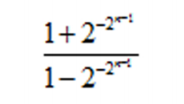
相似问题

• 如图1 正方体ABCDA′B′C′D′中 EE′∥FF′∥BB′ 平面AEE′A′与平面ABB′A′

  如图1,正方体ABCDA′B′C′D′中,EE′∥FF′∥BB′,平面AEE′A′与平面ABB′A′成15°角,平面AFF′A′与平面ADD′A′成30°角 如果正方体的棱长为1,那么

• 已知点M是△ABC所在平面内的一点 且满足MA2+MB2+MC2=4 那么△ABC三条边长之积AB·

  已知点M是△ABC所在平面内的一点,且满足MA2+MB2+MC2=4,那么△ABC三条边长之积AB·BC·CA的最大值是____

• 双曲线x2-y2/2 =1在点(-√2 √2)处的切线的方程是( ). (A)y=-x+√2.(B)

  双曲线x2-y2 2 =1在点(-√2,√2)处的切线的方程是( ) (A)y=-x+√2 (B)y=-x+3√2 (C)y=-2x-√2 (D)y=-2x+3√2

• 已知向量a b c是三个具有公共起点的非零向量 且|a|=2|b|=2 又a·b=-1 〈a-c

  已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π 3 ,则当|a-c|=7时,向量a与c的夹角是____

• 已知函数f(x)={(1-tan2x)/(1+tan2x)}2 则f(x)的最小正周期是( ).

  已知函数f(x)={(1-tan2x) (1+tan2x)}2 ,则f(x)的最小正周期是( ) (A)2π (B)3 2π (C)π (D)π 2