物体沿X轴做简谐振动 振幅为A 周期为T。试求出以下条件下质点的运动学方程。当t=0时 （1）物体在
物体沿X轴做简谐振动，振幅为A，周期为T。试求出以下条件下质点的运动学方程。当t=0时，（1）物体在x=A处。（2）物体在x=0处向正方向运动。（3）物体在x=－A/2处向正方向运动。
请帮忙给出正确答案和分析，谢谢！
参考解答
456***100
2024-11-03 21:56:00
正确答案：根据题意设质点的运动学方程为X=Acos(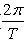
t+ψ) （1）当t=0时x=A。于是可得Acosψ=A （1）求解式（1）可得到 ψ=0 （2）因此该条件下质点的运动学方程为
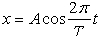（2）当t=0时x=0v＞0。于是可得Acosψ=0 -ωAsinψ＞0 （3）能同时满足式（3）的初相为
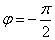因此该条件下质点的运动学方程为
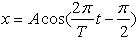（3）当t=0时x=-A/2v＞0。于是可得Acosψ=-A/2 -ωAsinψ＞0 （4）能同时满足式（4）的初相为
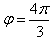因此该条件下质点的运动学方程为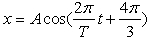
根据题意,设质点的运动学方程为X=Acos(t+ψ)（1）当t=0时,x=A。于是可得Acosψ=A（1）求解式（1）可得到ψ=0（2）因此,该条件下质点的运动学方程为（2）当t=0时,x=0,v＞0。于是可得Acosψ=0,-ωAsinψ＞0（3）能同时满足式（3）的初相为因此,该条件下质点的运动学方程为（3）当t=0时,x=-A/2,v＞0。于是可得Acosψ=-A/2,-ωAsinψ＞0（4）能同时满足式（4）的初相为因此,该条件下质点的运动学方程为
相似问题
当陀螺圆盘的转子的角加速度从零开始与时间成正比地增大时 经过5min后 转子以600πrad·s-1
当陀螺圆盘的转子的角加速度从零开始与时间成正比地增大时，经过5min后，转子以600πrad·s-1的角速度转动．试求转子在这段时间内转过的转数．请帮忙给出
如图4-8所示 两个小球用不能伸长的细软线连接 垂直地跨过固定在地面上 表面光滑的半径为R的圆柱 小
如图4-8所示，两个小球用不能伸长的细软线连接，垂直地跨过固定在地面上、表面光滑的半径为R的圆柱，小球B着地，小球A的质量为B的两倍，且恰与圆柱的轴心
如图7-5所示 A B为两个同振幅 同频率的相干波源 他们在同一介质中相距5λ/2 激起波的波长为λ
如图7-5所示，A、B为两个同振幅、同频率的相干波源，他们在同一介质中相距5λ 2，激起波的波长为λ，P为AB连线延长线上的一点。求：（1）自A、B两波源发
一个质点沿X轴做简谐振动 运动学方程为x=0.01cos(8πt+2π/3)（SI）。求此振动的振幅
一个质点沿X轴做简谐振动，运动学方程为x=0 01cos(8πt+2π 3)（SI）。求此振动的振幅、周期、速度的最大值和加速度的最大值。请帮忙给出正确答案和分析，谢谢！
一个转动惯量为200kg.m2的飞轮 在外力矩和轴承摩擦力矩作用下匀速转动 每分钟转180r。当外力
一个转动惯量为200kg m2的飞轮，在外力矩和轴承摩擦力矩作用下匀速转动，每分钟转180r。当外力矩停止作用后，飞轮经过两分钟停止转动。设轴承的摩擦力矩
