求解下列线性规划问题：max 2x1＋x2 S．t． x1＋x2≤5 x1一x2≥0 6x1＋2
求解下列线性规划问题：max 2x1＋x2 S．t． x1＋x2≤5， x1一x2≥0， 6x1＋2x2≤21， x1，
max 2x1+x2 S．t． x1+x2≤5， x1一x2≥0， 6x1+2x2≤21， x1，x2≥0．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-14 21:23:32
正确答案：引入松弛变量x3x4x5化成标准形式： max 2x1+x2 s．t．x1+x2+x3 =5 x1一x2 一x4 =0 6x1+2x2 +x5=21 xj≥0 j=12…5．用两阶段法求解．先求一个基本可行解为此引入人工变量y解下列线性规划： min y s．t． x1+x2+x3 =5 x1一x2 一x4 +y=0 6x1+2x2 +x5 =21 xj≥0 j=12…5 y≥0．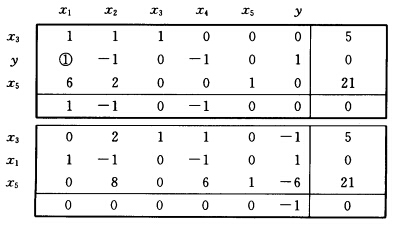
得到原线性规划的一个基本可行解．由此出发求最优解过程如下：
引入松弛变量x3,x4,x5,化成标准形式：max2x1+x2s．t．x1+x2+x3=5,x1一x2一x4=0,6x1+2x2+x5=21,xj≥0,j=1,2,…,5．用两阶段法求解．先求一个基本可行解,为此引入人工变量y,解下列线性规划：minys．t．x1+x2+x3=5,x1一x2一x4+y=0,6x1+2x2+x5=21,xj≥0,j=1,2,…,5,y≥0．得到原线性规划的一个基本可行解．由此出发求最优解,过程如下：
相似问题
计算积分计算积分其中C为： (1)连接原点O与点2＋i的直线段；． (2)连接原点O与点i的直线段计
计算积分计算积分其中C为： (1)连接原点O与点2＋i的直线段；． (2)连接原点O与点i的直线段计算积分其中C为： (1)连接原点O与点2+i的直线段；． (2)连
求下列函数的傅氏变换． 设F(ω)=[f(t)] 利用傅氏变换的性质求下列函数的傅氏变换． (1)f
求下列函数的傅氏变换． 设F(ω)=[f(t)]，利用傅氏变换的性质求下列函数的傅氏变换． (1)f设F(ω)=[f(t)]，利用傅氏变换的性质求下列函数的傅氏变换．
给定原问题 min 4x1+3x2+x3 s．t． x1一x2+x3≥1 x1+2x2-3x3≥2
给定原问题 min 4x1+3x2+x3 s．t． x1一x2+x3≥1， x1+2x2-3x3≥2， x1，x2，x3≥0． 已知对偶问题的最优解(ω1，ω2)=利用对偶性质求原问题的最
max 2x1+5x2 S．t． x1+2x2+x3 =16 2x1+x2+x4=12 xj≥0
max 2x1+5x2 S．t． x1+2x2+x3 =16， 2x1+x2+x4=12， xj≥0， j=1，2，3，4．请帮忙给出正确答案和分析，谢谢！
指出下列函数在零点z=0的级： 计算积分计算积分 请帮忙给出正确答案和分析 谢谢！
指出下列函数在零点z=0的级： 计算积分计算积分 请帮忙给出正确答案和分析，谢谢！
