证明f(z)=ez在复平面上解析 并求其导数．请帮忙给出正确答案和分析 谢谢！
证明f(z)=ez在复平面上解析，并求其导数．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-15 07:14:16
正确答案：f(z)=ez=ez(cos y+isin y)．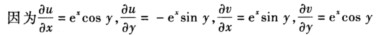 
四个偏导在复平面内均连续C．R．条件处处满足所以函数在复平面上处处可导处处解析． 由求导法则可得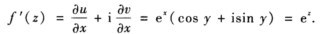 
f(z)=ez=ez(cosy+isiny)．四个偏导在复平面内均连续,C．R．条件处处满足,所以函数在复平面上处处可导,处处解析．由求导法则可得
相似问题
已知二次型f(x1 x2 x3)=x12+ax22+x32+2x1x2-2ax1x3-2x2x3的正
已知二次型f(x1，x2，x3)=x12+ax22+x32+2x1x2-2ax1x3-2x2x3的正、负惯性指数都是1，则a=( )．A．-2B．-1C．1D．2请帮忙给出正确答案和分析，谢谢！
计算下列函数的值： 请帮忙给出正确答案和分析 谢谢！
计算下列函数的值： 请帮忙给出正确答案和分析，谢谢！
设n阶实对称矩阵A满足条件A2+6A+8E=O 且A+tE是正定矩阵 则t的取值范围为_______
设n阶实对称矩阵A满足条件A2+6A+8E=O，且A+tE是正定矩阵，则t的取值范围为_______．请帮忙给出正确答案和分析，谢谢！
设A为3阶矩阵 r(A)=1 则λ=0( )．A．必定是A的二重特征值B．至少是A的二重特征值C．至
设A为3阶矩阵，r(A)=1，则λ=0( )．A．必定是A的二重特征值B．至少是A的二重特征值C．至多是A的二重特征值D．一、二、三重特征值均有可能请帮忙给出正确
二次型f(x1 x2 x3)=2x1x2+2x1x3+2x2x3的规范形为( )．A．2y12+y2
二次型f(x1，x2，x3)=2x1x2+2x1x3+2x2x3的规范形为( )．A．2y12+y22+y32B．y12-y22-y32C．2y12-y22-y32D．y12+y22+y32请帮忙给出正确答案和分析，谢谢！
